Teorema Bayes
Tulisan ini adalah pekerjaan rumah yang tertunda lebih dari setahun. Semua bermula dari sebuah rumus dalam tugas akhir kuliah.
![]()
Atau dalam dokumen yang sama (baca: laporan tugas akhir) disimplifikasi menjadi.
![]()
Sebaris rumus di atas adalah teorema Bayes yang dalam tugas akhir saya gunakan untuk mengelompokkan (klasifikasi) teks dari Twitter. Sebenernya diminta untuk kasih contoh perhitungan sederhana oleh dosen penguji proposal. Untungnya Pak Dosen ga menguji laporan akhir, jadi saya lolos tanpa tahu bagaimana cara menghitungnya deh, kwkwkw.
Beberapa hari ini entah kenapa berurusan lagi dengan Teori Bayes, karena itu sekalian saja dituliskan hasil perjalanan itu sebagai bentuk ‘mengumpulkan tugas’ dan pasti berguna sebagai future reference.
Versi wikipedia untuk rumus Bayes adalah adalah berikut (posisi Prior dan Likelihood ditukar).
![]()
Teori Bayes sendiri tujuan utamanya adalah menggambarkan hubungan antara peluang bersyarat dari dua kejadian dan , cukup membingungkan. Bagaimana jika diubah menjadi teori Bayes menghitung kemungkinan (probabilitas) terjadinya suatu peristiwa berdasarkan pengaruh yang didapat dari hasil observasi? Masih tak paham? Sama.
Ini yang lebih mudah dicerna, menurut wikipedia Teori Bayes menghitung kemungkinan terjadinya sebuah kejadian berdasarkan pengetahuan tentang kondisi yang mungkin berhubungan dengan kejadian tersebut. Contoh kasusnya begini.
Anda memiliki data apakah anak-anak di kampung Anda akan bermain bola di sore hari berdasarkan cuaca saat itu.
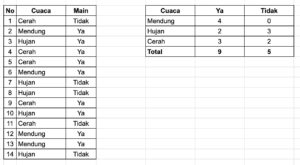
Jika ditanyakan pada Anda, berapa kemungkinan anak-anak di kampung akan bermain bola jika cuaca cerah, Anda dapat menggunakan rumus Bayes di atas.
![]()
Jika disesuaikan dengan contoh soal maka Posterior adalah kemungkinan anak-anak bermain bola berdasarkan data cuaca yang dimiliki. Posterior dapat dinotasikan seperti ini.
![]()
Dalam konteks soal, notasi tersebut bisa menjadi.
![]()
Prior adalah banyaknya kejadian, misal anak-anak bermain bola, yang kita duga saat kita belum punya data. Prior kejadian A dinotasikan seperti ini.
![]()
Jika kita diminta menebak berapa persen kemungkinan suatu lemparan koin akan menunjuk kepala (atau ekor), maka kita akan menduga 50% kemungkinan koin tersebut menunjuk kepala. Nilai 50% (1/2) tersebut adalah prior kita. Nilai itu adalah dugaan awal kita sebelum memiliki data lain mengenai koin tersebut. Misal setelah melakukan beberapa kali percobaan (pengamatan/observasi), belakangan kita tahu bahwa satu sisi koin ternyata lebih berat sehingga lebih mudah jatuh, di saat itu tentu kita akan mengubah prior.
Prior dalam konteks soal.
![]()
Jika menggunakan nilai dari tabel.
![]()
Likelihood adalah konsep yang rumit, likelihood bukanlah probabilitas tapi proporsional terhadap probabilitas. Likelihood dinotasikan seperti ini.
![]()
Dalam contoh soal.
![]()
Dengan nilai.
![]()
Evidence atau disebut pula Predictor Prior Probability adalah Prior kejadian B, dinotasikan.
![]()
Atau dalam konteks soal.
![]()
Dengan nilai.
![]()
Sehingga lengkapnya adalah.
![]()
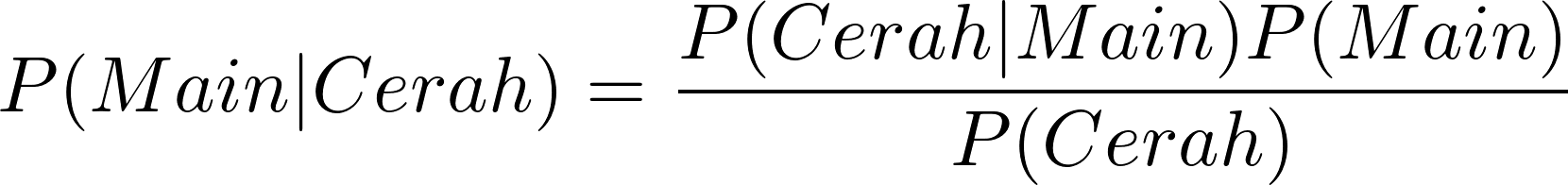
![]()
![]()
Simpulannya jika hari cerah maka kemungkinan 60% anak-anak akan bermain bola.
Sekarang kita akan mensimulasikan perhitungan lain. Dari data resmi Kemenkes ini diketahui bahwa pada tahun 2016 di Indonesia:
- Jumlah wanita 128.716.296 jiwa.
- Jumlah Ibu hamil 5.354.594 jiwa (4,16% dari jumlah wanita).
Jika ada test pack kehamilan dengan akurasi 99% maka berapa kemungkinan seorang wanita, dipilih secara acak, yang mendapat hasil test pack positif adalah benar-benar hamil?
Jika menemukan data seperti ini, teorema Bayes di atas dapat dimodifikasi dari yang semula seperti ini.
![]()
Penyebut dapat diubah menjadi.
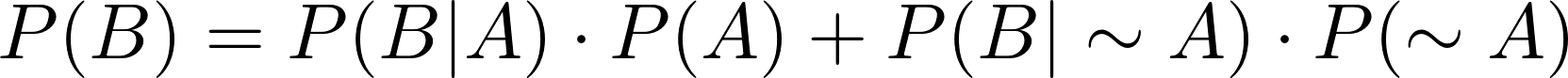
Sehingga menjadi.
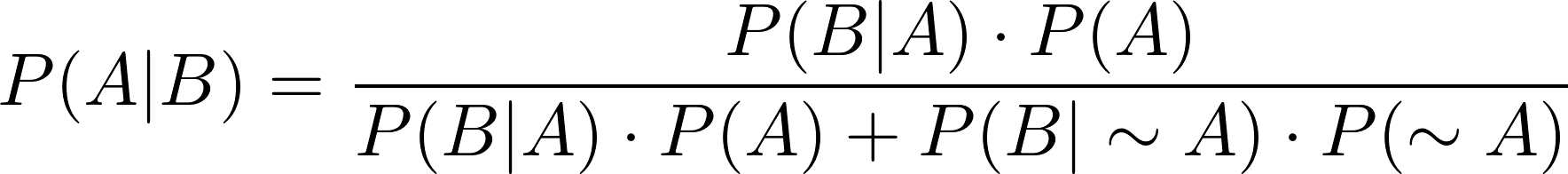
Dimana ![]() adalah kejadian bukan A.
adalah kejadian bukan A.
Omong-omong kita dapat menguji hasil perhitungan sebelumnya tentang anak-anak kampung bermain bola di hari cerah dengan rumus yang baru.
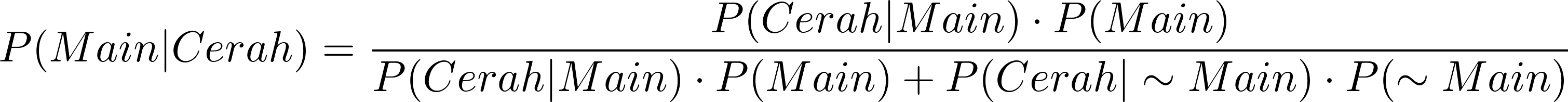
![]()
![]()
![]()
Hasilnya konsisten dengan metode sebelumnya.
Sekarang kita gunakan rumus yang baru untuk menguji kemungkinan menemukan wanita hamil yang hasil test pack-nya positif. Kali ini perhitungan menjadi lebih sederhana, cukup berbekal tingkat akurasi, persentase wanita hamil dan persentase wanita tidak hamil (1 – persentase wanita hamil).
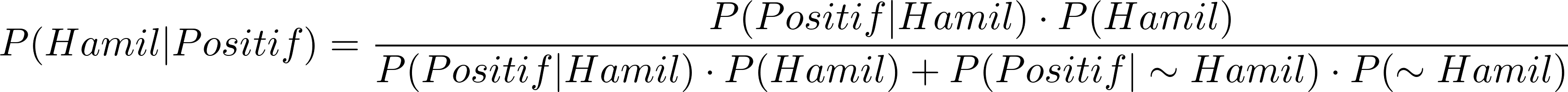
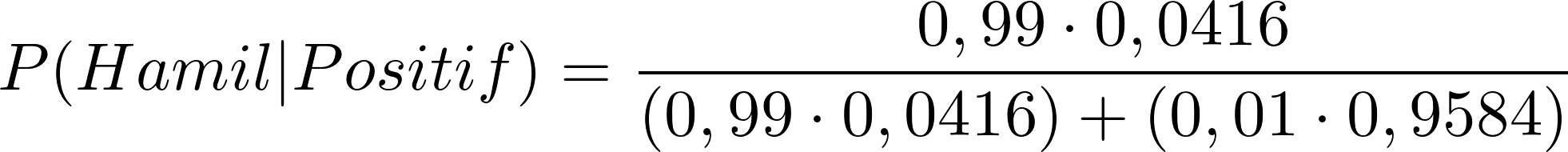
![]()
Jadi, di tahun 2016 jika kita memilih sembarang wanita, melakukan uji kehamilan menggunakan test pack dengan akurasi 99% dan hasilnya positif, maka kemungkinan wanita tersebut benar-benar hamil adalah 81,12%.
Kenapa hanya 81,12%? Tidak, katakanlah 99%, sesuai dengan tingkat akurasi test pack yang digunakan? Hal ini karena jumlah wanita tidak hamil yang besar, 95,84% dari populasi. Meski tingkat kesalahan test pack hanya 1% (100% – 99%) namun jika dikalikan dengan jumlah wanita tidak hamil tersebut maka hasilnya akan cukup signifikan. Misalnya dari 1.000 wanita, hanya 40 (4%) orang yang hamil, sisanya 960 (96%) orang tidak hamil. Test pack akan mendeteksi 960 x 1% sebagai positif hamil, maka terdapat minimal 9 orang yang salah dideteksi (false positive). Sehingga total akan dideteksi 49 wanita hamil padahal hanya terdapat 40 yang benar-benar hamil. Karena itu tidak perlu buru-buru membanjiri dumay dengan konten berjudul “Gempar, ternyata 99% hanya 81,12%!”, hehehe.
Pak Dosen, inilah perhitungan yang Bapak minta, meski terlambat mengumpulkannya, hehehe. Pada kesempatan selanjutnya akan dituliskan klasifikasi teks ala-ala menggunakan Naive Bayes.
Salam.
Contoh soal lain dapat dibaca di sini.
Lebih lanjut:
https://www.analyticsvidhya.com/blog/2017/09/naive-bayes-explained
https://en.wikipedia.org/wiki/Naive_Bayes_classifier
https://pythonmachinelearning.pro/text-classification-tutorial-with-naive-bayes/
https://sebastianraschka.com/Articles/2014_naive_bayes_1.html
https://www.saedsayad.com/naive_bayesian.htm
https://www.quora.com/What-is-the-difference-between-the-prior-and-the-posterior-in-statistics
https://en.wikipedia.org/wiki/Posterior_probability
https://becominghuman.ai/naive-bayes-theorem-d8854a41ea08

2 Replies to “Teorema Bayes”