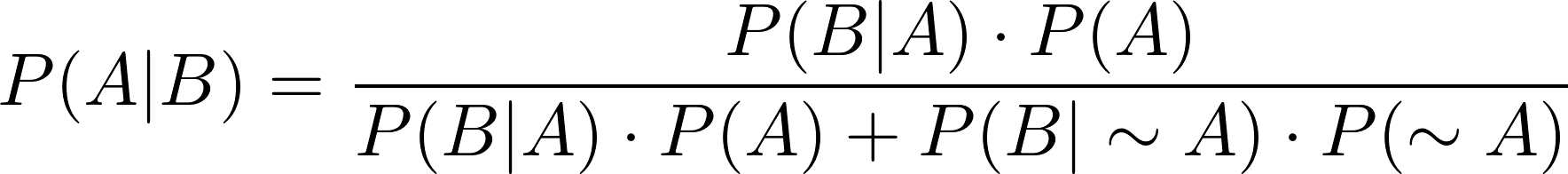
Teorema Bayes di Dunia Nyata - Contoh Soal

Di bangku sekolah kita sering punya pertanyaan filosofis tentang kehidupan, seperti “apa gunanya semua rumus matematika ini, yang dibaca saja sulit, apalagi dikerjakan?”. Kali ini kita akan menjawab salah satunya, apa gunanya Teorema Bayes di dunia nyata.

Bagi pembaca yang perlu sedikit pemanasan mengenai Bayes, sila membaca tulisan pertama mengenainya. Dari sana kita akan mengambil formulanya saja.

$P(A | B) = \frac{P(B | A) P(A)}{P(B)}$

Formula di atas kita namakan Rumus A. Jika kita memiliki variabel kejadian bukan A ( $\sim A$ ) maka formula yang digunakan adalah.

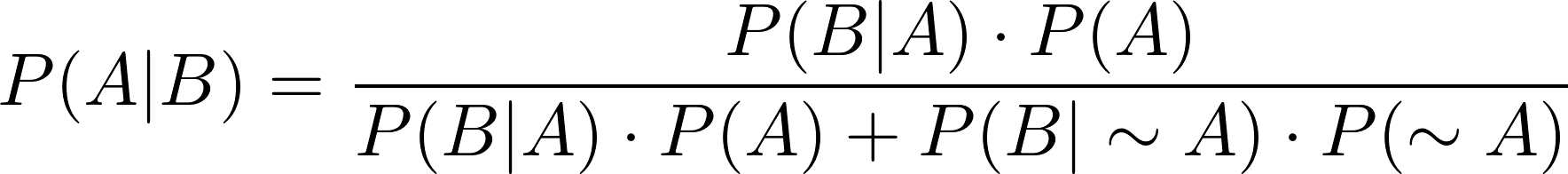
Kita namakan Rumus B untuk formula di atas.

Ini adalah rangkaian tulisan yang dibagi menjadi 2, pertama (tulisan ini) kita akan membahas contoh soal (seperti di kelas), mengambil soal dari sini, biar bagaimanapun mengerjakan soal di kelas juga merupakan persoalan dunia nyata, kan? Hehehe. Pada bagian kedua kita akan mendiskusikan penggunaan “lebih serius” dari bidang ekonomi, yaitu pendeteksian fraud menggunakan Naive Bayes.

Di bagian pertama ini ada 5 soal yang perlu dikerjakan.

1. Kit Uji Penyakit

Pada penyakit yang diderita oleh 0,1% populasi penduduk terdapat sebuat alat uji dengan akurasi 99% mendeteksi penderita penyakit tersebut. Namun alat tersebut memiliki kemungkinan 0,5% false positive, yaitu salah mendeteksi orang tidak sakit namun dideteksi sakit. Jika seseorang dideteksi sakit oleh alat ini, sebenarnya berapa persen kemungkinan ia benar-benar sakit?

Jawaban:

Kita menggunakan Rumus B untuk menyelesaikannya.

$P(Sakit|Positif) = \frac{0,99 \cdot 0,001}{0,99 \cdot 0,001 + 0,005 \cdot 0,999}$

$P(Sakit|Positif) = 0,1654135338 = 16,54\%$

Cukup jelas, variabel telah disediakan oleh soal, yang mana peluang (hasil) positif adalah benar-benar sakit, berapa yang dianggap positif namun tidak benar-benar sakit. Peluang tidak sakit $P(\sim Sakit)$ adalah $100\% - 0,1\% = 99,9\% = 0,999$ .

2. Produk Rusak

Dua lini produksi membuat produk yang sama. Lini 1 membuat 1.000 produk/minggu dengan 100 diantaranya rusak. Lini 2 membuat 2.000 produk/minggu dengan 150 rusak. Jika kita memilih produk secara acak, berapa kemungkinan produk itu rusak? Jika rusak, berapa kemungkinan produk tersebut dibuat oleh Lini 1?

Jawaban:

Atau jika $\sim Lini_1$ diganti menjadi $Lini_2$ .

$P(Lini_1|Rusak) = \frac{\frac{100}{1.000} \cdot \frac{1.000}{3.000}}{\frac{100}{1.000} \cdot \frac{1.000}{3.000} + \frac{150}{2.000} \cdot \frac{2.000}{3.000}}$

$P(Lini_1|Rusak) = \frac{\frac{1}{30}}{\frac{1}{30} + \frac{1}{20}} = \frac{2}{5}$

3. Prakiraan Cuaca

Besok Marie akan mengadakan resepsi di luar gedung, sayangnya prakiraan cuaca bilang besok hujan. Sebenarnya di tahun-tahun belakangan ini hujan hanya turun 5 hari/tahun. Selama ini, jika benar-benar hujan, prakirawan cuaca memprediksi dengan benar sebesar 90%. Jika tidak hujan, prakirawan salah memprediksi sebanyak 10% (dari semua prediksi yang telah dibuat). Jadi berapa kemungkinan besok benar-benar hujan? (Diasumsikan tidak ada tahun kabisat).

Jawaban:

$P(Hujan|PrediksiHujan) = \frac{\frac{90}{100} \cdot \frac{5}{365}}{\frac{90}{100} \cdot \frac{5}{365} + \frac{10}{100} \cdot \frac{360}{365}}$

$P(Hujan|PrediksiHujan) = \frac{\frac{9}{730}}{\frac{9}{730} + \frac{360}{365}} = \frac{1}{9}$

4. Pengguna Produk

Anda menjual produk di daerah dimana 30% adalah tinggal di tengah kota dan sisanya tinggal di pinggir kota. Saat ini 20% penduduk kota menggunakan produk tersebut, dan sebanyak 10% penduduk pinggir kota menggunakannya. Anda diberikan 2 strategi pemasaran baru, strategi pertama meningkatkan market share di pinggir kota menjadi 15%. Strategi kedua meningkatkan market share di tengah kota menjadi 25%. Strategi mana yang akan diadopsi? Sebelum strategi baru diterapkan, berapa kemungkinan persen pengguna produk, yang Anda temui, ternyata adalah penduduk kota?

Jawaban:

$StrategiA = \frac{\frac{15}{100} \cdot \frac{70}{100}}{\frac{15}{100} \cdot \frac{70}{100} + \frac{25}{100} \cdot \frac{30}{100}}$

$StrategiA = \frac{\frac{21}{200}}{\frac{21}{200} + \frac{3}{40}} = \frac{7}{12}$

$StrategiB = \frac{\frac{25}{100} \cdot \frac{30}{100}}{\frac{25}{100} \cdot \frac{30}{100} + \frac{15}{100} \cdot \frac{70}{100}}$

$StrategiB = \frac{\frac{3}{40}}{\frac{3}{40} + \frac{21}{200}} = \frac{5}{12}$

Strategi Kedua (StrategiB) lebih kecil ( $\frac{5}{12}$ ) dari yang pertama ( $\frac{7}{12}$ ). Atau lebih mudah dipahami $StrategiA > StrategiB$ . Sekarang kita hitung berapa persen kemungkinan pengguna produk, yang secara acak Anda temui, adalah penduduk kota.

$P(Kota|Pengguna) = \frac{\frac{20}{100} \cdot \frac{30}{100}}{\frac{20}{100} \cdot \frac{30}{100} + \frac{10}{100} \cdot \frac{70}{100}}$

$P(Hujan|PrediksiHujan) = \frac{\frac{6}{100}}{\frac{6}{100} + \frac{7}{100}} = \frac{6}{13}$

5. Mesin Jackpot

Di sebuah arena permainan (FunStation/FunWorld/KidCity/TimeZone) terdapat 2 mesin permainan yang mengeluarkan tiket yang bisa ditukar dengan hadiah. Mesin pertama telah mengeluarkan jackpot sebanyak 10% sepanjang waktu, sedang mesin kedua 20%. Tentu kita akan memilih yang mengeluarkan jackpot sebanyak 20%, namun kita tidak tahu mesin mana yang pertama, mana yang kedua. Akhirnya kita membuat asumsi bahwa kedua mesin di depan kita sama baik hatinya. Kita pilih salah satu, secara acak, lalu memasukkan koin/menggesek kartu. Jika pada kesempatan pertama kita gagal, sebenarnya berapa kemungkinan kita telah menggunakan mesin kedua yang lebih pemurah?

Jawaban:

$P(Mesin_2|GagalJackpot) = \frac{\frac{80}{100} \cdot \frac{50}{100}}{\frac{80}{100} \cdot \frac{50}{100} + \frac{90}{100} \cdot \frac{50}{100}}$

$P(Mesin_2|GagalJackpot) = \frac{\frac{40}{100}}{\frac{40}{100} + \frac{45}{100}} = \frac{8}{17}$

Sampai jumpa di bagian kedua, salam.

Teorema Bayes di Dunia Nyata – Contoh Soal

1. Kit Uji Penyakit

2. Produk Rusak

3. Prakiraan Cuaca

4. Pengguna Produk

5. Mesin Jackpot

Lebih Lanjut:

Published by Aan Subarkah

One Reply to “Teorema Bayes di Dunia Nyata – Contoh Soal”

Leave a Reply Cancel reply