Klasifikasi Teks dengan Naive Bayes

Jika menemukan orang yang menyatakan matematika itu mudah, segera jauhi, kemungkinan ia aneh. Kwkwkw.
Tapi sungguh, matematika adalah bagian penting dalam kehidupan kita yang tidak mungkin terhindarkan. Bahkan di bagian yang menurut kita tidak berhubungan dengannya, matematika ternyata berperan penting. Seperti soalan yang akan kita bahas.
Melanjutkan tulisan sebelumnya mengenai Teorema Bayes, kali ini akan dibahas bagaimana melakukan klasifikasi teks menggunakan Naive Bayes.
![]()
Untuk apa kita perlu melakukan klasifikasi teks?
Klasifikasi teks adalah jamak dilakukan di era industry 4.0 ini. Kita telah menggunakan (atau merasakan manfaatnya) bahkan tanpa kita sadari. Brand (dalam bentuk apapun, misal tokoh politik) menggunakan klasifikasi teks untuk menjaring opini publik, misal suka atau tidak suka dengan produk (atau kebijakan atau tema kampanye). Kantor berita online mengklasifikasi berita menjadi Politik, Ekonomi, Teknologi, dan lain sebagainya, dengan bantuan komputer yang mendayagunakan konsep yang sama. Penyedia layanan melakukan klasifikasi email masuk untuk menentukan apakah surat tersebut adalah spam atau bukan.
Bahkan kita dapat memberdayakan sistem sederhana untuk mengklasifikasi teks, misalnya menentukan apakah artikel berita online (atau thread di forum) baru memuat tema yang kita senangi atau tidak. Apakah suatu tweet relevan dengan tema akun atau hanya berupa iklan. Banyak yang dapat dilakukan dengan klasifikasi teks, dan kebutuhan kita pasti akan mendorong kreatifitas.
Oya, kita akan sampai pada penjelasan kenapa ada tambahan kata naive pada teorema Bayes kita, namun pertama-tama kita perlu mengkonversi teks menjadi kata agar perhitungan dari teks dapat dilakukan. Untuk melakukannya terdapat beberapa metode seperti Bag of Words, tf-idf dan beberapa lainnya. Di bawah ini akan diceritakan sedikit tentang Bag of Words (BoW) dan tf-idf, lalu BoW akan digunakan pada proses klasifikasi teks.
Bag of Words (BoW)
Terdapat dua teks.
- Ini ibu Budi.
- Ibu Budi pergi ke pasar bersama Budi.
BoW, seperti namanya, adalah sebuah tas (kresek) berisi semua kata pada teks yang akan diproses. Pertama teks (atau kalimat) dibagi menjadi beberapa bagian, proses ini diistilahkan tokenization. Pada proses ini yang diambil hanya kata, tanda baca tidak.

Tiap kolom merepresentasikan kata dan baris adalah jumlah kemunculan kata tersebut pada teks. Tiap baris pada tabel di atas dapat juga diistilahkan sebagai vektor. Pada teks pertama kita mendapatkan sebuah vektor [1, 1, 1, 0, 0, 0, 0], [0, 1, 2, 1, 1, 1, 1] pada baris kedua dan begitu seterusnya.
Ada variasi lain dari BoW yaitu dengan mengambil sebanyak n kata untuk tiap kolom (kolom diistilahkan pula sebagai feature), konsep ini disebut n-gram. Contoh di atas menggunakan satu kata, diistilahkan unigram. Jika menggunakan dua kata (bigram) maka kolom akan menjadi:
- ini ibu
- ibu budi
Dan untuk teks kedua.
- ibu budi
- budi pergi
- pergi ke
- ke pasar
- pasar bersama
- bersama budi
Kapan menggunakan unigram dan kapan n-gram (dan seberapa banyak n) amat bergantung pada studi kasus yang dihadapi, silahkan mencoba sendiri berapa banyak n yang efektif.
tf-idf
Term Frequency-Inverse Document Frequency (tf-idf), sesuai nama, padanya terdapat dua langkah yaitu menghitung kemunculan term (kata) pada suatu dokumen dan menghitung kemunculan term pada seluruh dokumen. Kemudian hasil dari dua langkah tersebut dikalikan, jadi kalau di pikir sebenarnya ada tiga langkah, pernyataan dua langkah di atas tidak valid, hehehe.
Dokumen di sini dapat sebuah kalimat, seperti contoh ibu Budi di atas, atau sebuah teks panjang seperti sehalaman blog ini. Intinya yang disebut dokumen adalah sekumpulan term.
Proses kedua (idf) melibatkan pembalikan (inverse) sehingga sebuah term yang jarang ditemukan pada dokumen akan memiliki nilai lebih tinggi ketimbang term yang banyak ditemukan.
Untuk menghitung kemunculan kata (tf) kita hanya perlu menghitung jumlah kemunculan term (kata) dibagi dengan jumlah total term pada dokumen, dinotasikan sebagai berikut.
(1) 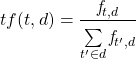
Dan, gambar di awal tulisan ini menjadi relevan, kwkwkw.
Mari kita cerna perlahan.
- tf = term frequency a.k.a frekuensi kemunculan tiap kata
- t = term (kata)
- d = document (dokumen/kumpulan teks)
Kita gunakan contoh yang sama seperti di bagian sebelumnya, ibu Budi.
- Ini ibu Budi.
- Ibu Budi pergi ke pasar bersama Budi.
Di atas adalah dua dokumen, dokumen 1 (d1) dan dokumen 2 (d2).
Term Frequency kata ini pada dokumen pertama adalah.
(2) 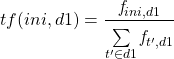
(3) ![]()
Sesederhana itu, banyaknya kata ini dibagi dengan total kata pada dokumen. Sehingga nilai tf pada dua dokumen di atas adalah seperti ini.

IDF dilakukan dengan menghitung jumlah seluruh dokumen dibagi dengan jumlah semua dokumen yang mengandung term tertentu. Menggunakan contoh di atas, berikut nilai idf kata ini dan ibu.
![]()
![]()
Seperti terlihat, kata ini yang hanya terdapat pada satu dokumen memiliki nilai idf lebih besar ketimbang kata ibu yang muncul di dua dokumen. Hal tersebutlah yang membuat ada kata inverse dalam idf, makin jarang ditemukan suatu kata maka nilainya makin tinggi alih-alih makin rendah.
Dalam contoh kita hanya menggunakan dua dokumen, bagaimana kalau kita punya 100 dokumen, 1000, 10.000, sejuta, atau sejuta ribu, atau sejuta ribu-ribu-ribu-juta? Misal pada 1.000.000 dokumen, kata ini muncul di 100.000 dokumen tapi kata ibu hanya terdapat pada 2 dokumen.
![]()
![]()
Terlalu tidak imbang, 10 vs 500.000.
And….. log come to the rescue!
Menggunakan log (basis 10) kita dapat memperkecil beda nilai idf di atas.
![]()
![]()
Terimakasih log, akhirnya engkau terlihat masuk akal dan berguna sekarang, kwkwkw.
Buat saya, yang bukan pecinta matematika, selain penggunaan huruf (sesuai gambar), hal kedua yang mengintimidasi dari matematika adalah log. Ekspresi pertama saat melihat kata log dalam perhitungan adalah putus asa.
Kembali ke idf, sejauh ini formula perhitungan idf dapat dinotasikan seperti ini.
(4) ![]()
Meski masih lumayan menakutkan, namun sekarang rumus di atas sedikit banyak dapat kita interpretasikan.
- idf (t, D): hitung nilai idf dari suatu kata “t” pada semua dokumen.
- log: seimbangkan angka yang terlalu tinggi dan terlalu rendah, seperti contoh 10 vs 500.000 di atas.
- N: jumlah semua dokumen.
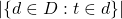 : jumlah dokumen yang mengandung kata “t”.
: jumlah dokumen yang mengandung kata “t”.
Sekarang bagaimana bila kita mencari term yang ternyata tidak ada dalam dokumen, misal kata kwkwkw.
![]()
Adalah pengetahuan bersama bahwa kita tidak dapat membagi angka berapapun dengan nol (nol bahkan bukan angka). Demikian pula dengan log(0) akan menghasilkan yang sama, undefined.
Lalu bagaimana mengatasi kondisi di atas, term yang kita cari tidak ada dalam dokumen manapun yang kita punya tapi kita tidak ingin perhitungan menjadi undefined.
Tambahkan angka satu (1) pada perhitungan. Dimana menambahkan angka tersebut? Terdapat beberapa alternatif. Wikipedia mencontohkan 2 alternatif.
Pertama pada penyebut (angka di bawah tanda bagi) dari semula ![]() menjadi
menjadi ![]() sehingga formula menjadi.
sehingga formula menjadi.
(5) ![]()
Alternatif kedua tambahkan pada log.
(6) ![]()
Dan ada alternatif ketiga dimana angka 1 ditambahkan sebelum log sehingga kita akan mendapatkan setidaknya nilai 1 pada idf.
(7) ![]()
Namum umumnya perhitungan tidak melibatkan penambahan angka 1 di atas, cukup nilai log jumlah dokumen dibagi dokumen yang mengandung kata “t”.
(8) ![]()
Atau kadang diringkas menjadi.
(9) ![]()
Nilai tf dan idf pada contoh soal menjadi seperti ini.

Setelah mendapatkan nilai tf dan idf sekarang tinggal mengalikan dua nilai tersebut untuk mendapatkan tf-idf.
(10) ![]()

Klasifikasi Teks
Kata naive pada Naive Bayes muncul dari kenaifan metode ini yang menganggap semua kata dalam dokumen adalah independen satu dengan lainnya, tiap kata dibobot sama. Padahal tidak sesederhana itu, misal kata langit dan tentu memiliki makna yang berbeda dengan langit-langit. Kata tidak dan bisa tentu berbeda jika ditampilkan sebagai dua kata terpisah (tidak dan bisa) atau satu frasa (tidak bisa). Ibu Budi di atas juga bermakna berbeda dengan ibu dan Budi.
Menariknya meski menanggung ketidakakuratan asumsi itu, metode Naive Bayes efektif dalam klasifikasi teks. Dan pula relatif efisien ketimbang metode lain.
Dalam klasifikasi teks, kita memberikan pada sistem beberapa kalimat yang telah diberi label berupa kelas negatif atau positif. Setelahnya kita berikan kalimat baru yang harus diberi label oleh sistem, apakah masuk kelas negatif atau positif.
Kita akan mensimulasikan Naive Bayes untuk mengklasifikasi review pembeli di e-commerce, dua klasifikasi digunakan, positif dan negatif.
Sebagai ilustrasi, kita mendapatkan 10 reviu produk dimana 7 adalah positif dan 3 negatif.
Reviu positif:
- barangnya bagus, respon penjual cepat
- top seller
- biarkan bintang berbicara
- pesan minggu senin sampe
- sesuai espektasi
- terimakasih barang sudah sampai dengan selamat
- prduk sesuai deskripsi, makasih
Reviu negatif:
- mengecewakan penyok ujungnya
- ternyata rapuh sekali, nyesel dah beli 2
- pesen warna merah yang datang biru bukan merah
Karena terdapat 7 reviu (document) positif dari total 10 maka probabilitas reviu positif adalah ![]() dan probabilitas reviu negatif
dan probabilitas reviu negatif ![]() .
.
Langkah kerja yang dilakukan diadopsi dari buku Machine Learningnya om Tom Mitchell dan dijelaskan dengan sangat baik oleh mas Fransisco Lacobelli.
Pertama kita membuat Bag of Words dari semua dokumen.

Banyak betul kolomnya, ya. Benul eh betul. Ada beberapa metode untuk mengurangi banyak kolom (features) itu, antara lain:
- Spelling correction, mengganti kata yang keliru penulisannya, misal kata sampe (positif 4) diganti agar sama dengan sampai (positif 6). Kata dah (negatif 2) menjadi sudah (positif 6).
- Lemmatisation, beberapa kata bermakna sama dikelompokkan menjadi satu, seperti kata terimakasih (positif 6) dan makasih (positif 7).
- Stemming, mengubah kata berimbuhan menjadi kata dasar, kata barangnya (positif 1) menjadi barang (positif 6).
Namun metode-metode tersebut perlu waktu untuk pemrosesan, sehingga penggunaannya harus mempertimbangkan cost and benefit. Saya sangat menyarankan untuk mencoba sendiri efektifitas metode yang akan digunakan karena saya sendiri menemukan bahwa penambahan metode tidak selalu menghasilkan output yang lebih baik.
(11) ![]()
Kembali ke BoW reviu produk, kita akan menghitung probabilitas kata akan muncul dalam kelas (reviu) positif dan negatif menggunakan rumus di atas, dimana:
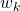 adalah kata (word) k dalam semua dokumen (reviu) yang diberi label sebagai j (positif/negatif).
adalah kata (word) k dalam semua dokumen (reviu) yang diberi label sebagai j (positif/negatif).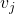 semua kata (vocabulary) dalam kelas j (positif/negatif).
semua kata (vocabulary) dalam kelas j (positif/negatif).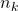 berapa kali suatu kata muncul dalam kelas j.
berapa kali suatu kata muncul dalam kelas j.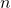 banyak kata dalam kelas j.
banyak kata dalam kelas j.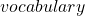 total kata unik dalam semua dokumen.
total kata unik dalam semua dokumen.
(12) ![]()
(13) ![]()
(14) ![]()
(15) ![]()
(16) ![]()
(17) ![]()
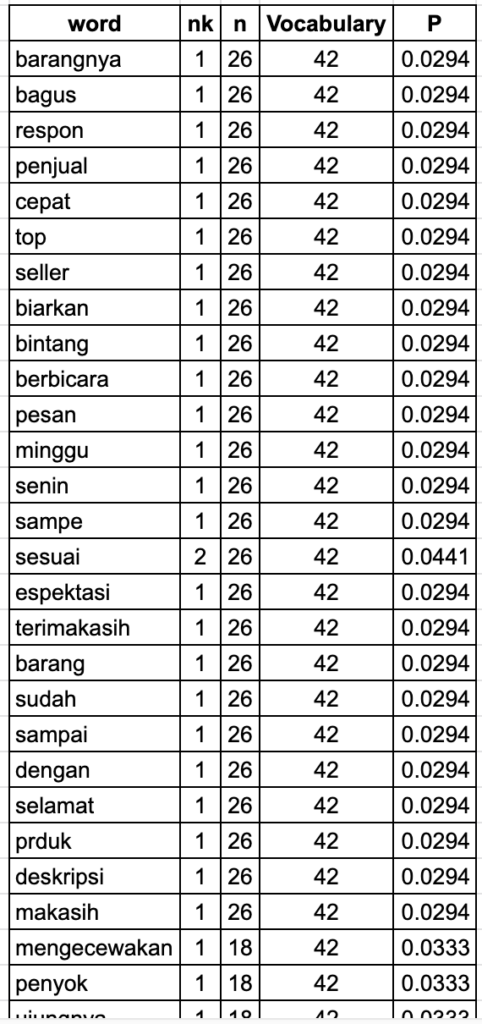
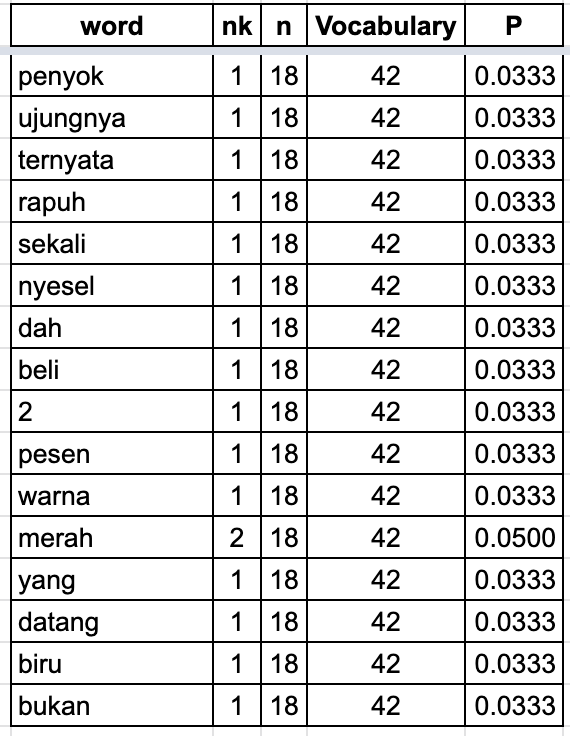
Nilai probabilitas tiap kata pada tiap kelas adalah sebagai berikut.
Di atas adalah proses mempelajari dokumen pada tiap kelas, sekarang saatnya menggunakan hasil belajar itu untuk melakukan klasifikasi dokumen baru. Formula yang digunakan adalah seperti ini (alasan pemilihan formula ini akan dibahas di kesempatan mendatang).
(18) ![]()
Formula di atas, singkatnya menyatakan bahwa nilai (value) Naive Bayes yang digunakan adalah nilai tertinggi dari hasil perkalian probabilitas kelas dan probabilitas tiap kata pada suatu kelas.
sebagai contoh, terdapat reviu baru.
barangnya top, sampe dengan selamat
Dihitung nilai Naive Bayes pada kelas positif dan negatif.
Positif:
(19) ![]()
(20) ![]()
Negatif:
(21) ![]()
(22) ![]()
Nilai kelas positif lebih tinggi (![]() ) ketimbang kelas negatif (
) ketimbang kelas negatif (![]() ) sehingga “barangnya top, sampe dengan selamat” diklasifikasikan sebagai reviu positif.
) sehingga “barangnya top, sampe dengan selamat” diklasifikasikan sebagai reviu positif.
Menarik bukan, ternyata matematika memungkinkan kita memilah mana sentimen positif dan mana negatif dari suatu kalimat.
Salam.
Lebih lanjut:
- https://sebastianraschka.com/Articles/2014_naive_bayes_1.html
- https://medium.freecodecamp.org/how-to-process-textual-data-using-tf-idf-in-python-cd2bbc0a94a3
- https://medium.com/@paritosh_30025/natural-language-processing-text-data-vectorization-af2520529cf7
- http://www.tfidf.com/
- https://www.youtube.com/watch?v=EGKeC2S44Rs
- Machine Learning by Tom M. Mitchell
- A Probabilistic Analysis of the Rocchio Algorithm with TFIDF for Text Categorization by Thorsten Joachims
- Beyond Independence: Conditions for the Optimality of the Simple Bayesian Classifier by Pedro Domingos and Michael Pazzani

blognya bagus kak, penjelasannya juga bagus, simple, dan mudah dimengerti. tapi gambarnya kenapa tidak found semua, jadi ada beberapa pemahaman yang miss..
Hai, terimakasih telah membaca tulisan ini, saat ini kami memiliki sedikit kendala teknis pada tabel yang ditampilkan pada tulisan ini sehingga sedikit mengganggu bagi pembaca. Kami sedang mengupayakan perbaikan untuk itu, semoga tidak memakan waktu lama.
Halo kak mau bertanya, itukan pembobotan di implementasinya menggunakan Bag of words sebelum NBC. Kalau pakai TF IDF sebelum NBC bagaimana ya? Terima kasih
kemaren situs ini down kenapa min?
Hehehe, iya, nih, servernya perlu maintenis. Terimakasih perhatiannya. Omong-omong tema tulisan apa yang diminati?
semua tulisannya menarik min