
Statistical Distributions – The Binomial Distribution
Enggan mendayung, hanyut serantau.
Ini jenis tema yang kita tak dapat lari darinya, tidak dapat digunakan secara instan namun melewatkannya bakal membuat sebuah lubang besar pada pemahaman kita.
Pemahaman mengenai distribusi statistik akan terus kita gunakan kapanpun, selama berurusan dengan data. Karenanya, enggan mendayung, hanyut serantau.
Tulisan ini adalah kelanjutan dari tulisan soal variasi data (statistika deskriptif) bedanya distribusi data berhubungan dengan statistika inferensi alih-alih statistika deskriptif.
Statistika Inferensial
Menurut bu Navaro di Learning Statistics with R (rujukan utama tulisan statistik di laman ini), statistika inferensi adalah apa yang bisa kita pelajari dari apa yang sudah kita tahu. Sedangkan halaman pertama dari hasil pencarian “statistika inferensial” pada mesin pencari menghasilkan definisi antara lain:
- Semua metode yang berhubungan dengan analisis sebagian data atau juga sering disebut dengan sampel untuk kemudian sampai pada peramalan atau penarikan kesimpulan mengenai keseluruhan data induknya (populasi).
- Metode yang mampu dipakai untuk menganalisis kelompok kecil dari data induknya atau sample yang diambil dari populasi sampai pada peramalan dan penarikan kesimpulan pada kelompok data induknya atau populasi.
- Teknik analisis data yang digunakan untuk menentukan sejauh mana kesamaan antara hasil yang diperoleh dari suatu sampel dengan hasil yang akan didapat pada populasi secara keseluruhan.
- Proses pengambilan kesimpulan-kesimpulan berdasarkan data sampel yang lebih sedikit menjadi kesimpulan yang lebih umum untuk sebuah populasi
Jika dirangkum dari pelbagai definisi tersebut, kata kunci untuk tema statistika inferensial adalah metode, sampel, simpulan dan populasi, sila membuat definisi sendiri untuk membangun intuisi mengenai topik tersebut. Misal menyimpulkan bahwa statistika inferensial adalah metode yang digunakan menyimpulkan populasi berdasarkan sampel. Atau yang agak spesifik, metode pengambilan sampel untuk dapat menyimpulkan populasi, juga bisa. Masing-masing memiliki nilai kebenarannya sendiri.
Sampel
Kenapa sampel? Karena kita (siapapun) tidak punya cukup sumberdaya (waktu, tenaga, biaya) untuk mendapatkan data dari populasi.
Sebagai akibat karena “hanya” sampel maka terdapat jarak (gap) dengan populasi.
Diilustrasikan seperti ini. Dari 273.630.147 penduduk Indonesia (versi worldometers yang diakses pada 13 Juli 2020 pukul 21:16 WIB, data ini sendiri juga merupakan estimasi) kita ingin tahu apakah jumlah pecinta makan bubur ayam diaduk sama dengan penggemar makan bubur ayam tanpa diaduk.
Sudah terang tidak ada yang dapat membiayai prosedur wawancara pada 273juta populasi Indonesia, karenanya kita mengambil sampel, katakanlah 1.000 orang yang diambil secara acak. Dari seribu orang tersebut akhirnya diketahui bahwa 51,99% memilih diaduk dan sisanya sekitar 48,01% berideologi tanpa diaduk.
Lalu kita simpulkan bahwa mayoritas penduduk Indonesia, yang berjumlah 273juta itu, tepatnya 51,99%, berkeyakinan makan bubur ayam diaduk adalah kebenaran mutlak yang tak perlu disangsikan.
Bila entah bagaimana kita dapat melakukan wawancara pada seluruh penduduk Indonesia, belum tentu sebanyak 51,99% menyatakan akan makan bubur dengan diaduk. Bisa saja hanya 45,87% yang memilih sikap hidup tersebut, atau 69,90% yang setuju dengan itu, atau bisa juga malah sebanyak 50%.
Jika angka terakhir yang benar, maka pertanyaan besar kita terjawab dengan, benar bahwa pecinta makan bubur diaduk sama banyak dengan tanpa diaduk.
Jika ternyata angka yang benar adalah 45,87%, maka ada celah antara 51,99% dan 45,87%.
Statistika inferensial menyediakan alat untuk berbagai kepentingan seperti memperkecil celah tersebut, memprediksi besaran celah, bahkan menyatakan bahwa pertanyaan tersebut (apakah orang Indonesia yang suka makan bubur diaduk sejumlah dengan orang yang suka makan bubur tanpa diaduk) ternyata salah.
Statistika inferensial berdiri di atas teori peluang. Peluang/probabilitas adalah nilai yang menunjukkan kemungkinan terjadinya suatu kejadian. Nilai tersebut berkisar 0 sampai 1. Misal pada uang koin, peluang mendapatkan kepala adalah 0,5 (50%), peluang mendapatkan angka 1 pada dadu adalah ![]() (16,67%).
(16,67%).
Teori peluang adalah konsep yang lebih rumit, kita lewatkan saja (terutama karena penulis tidak paham).

Distribusi Statistik
Kita lompat ke distribusi peluang, atau sesuai judul, distribusi statistik. Namun sebelumnya akan dijelaskan beberapa terminologi yang kerap digunakan.
Misal kita melempar sebuah koin sebanyak dua kali dengan hasil seperti ini (H = Head, T = Tail).
![]()
Meskipun dalam kejadian tadi hanya menghasilkan H dan T namun sebenarnya terdapat empat kemungkinan dalam eksperimen kita, yaitu.
![]()
S di atas adalah sample space, ruang sampel, yaitu set (himpunan) seluruh hasil yang mungkin terjadi dalam experiment (percobaan). Ruang sampel selain disimbolkan ![]() sering pula menggunakan
sering pula menggunakan ![]() .
.
Masing-masing kejadian dalam sample space, misal HH atau HT, disebut elementary event.
Elementary event ini memiliki peluang ![]() dengan rumus.
dengan rumus.
![]()
Satu kejadian dibagi dengan jumlah anggota dalam ruang sampel. Jadi, kejadian HH memiliki peluang 0.25.
![]()
![]()
Definisi distribusi statistik menurut wikipedia adalah fungsi matematika yang menyediakan (daftar) kemungkinan kemunculan outcome (suatu nilai) dalam sebuah eksperimen.
Menyebut distribusi statistik maka umumnya akan teringat pada “distribusi normal”, namun tulisan ini akan membahas jenis yang lain.

Binomial Distribution
Bernoulli Trials
Satu percubaan yang mantap dalam pelemparan koin akan menghasilkan dua kemungkinan yaitu kepala dan ekor. Contoh lain, dalam pertandingan kita punya dua kemungkinan, menang atau kalah.
Percobaan seperti di atas, yang hanya memiliki dua kemungkinan dinamakan Bernoulli Trial. Umumnya salah satu kemungkinan akan dilabeli success dan satunya lagi failure. Misal dalam pelemparan koin, kepala dapat dilabel sebagai success dan ekor sebagai failure.
Bernoulli Distribution
Lalu berapa peluang mendapatkan success dan failure? Saat melempar koin (yang fair) peluang mendapatkan kepala (success) adalah ![]() .
.
![]()
Sehingga peluang mendapat ekor (failure) adalah.
![]()
![]()
![]()
Karena hanya perlu dua kemungkinan, success (disimbolkan ![]() ) dan failure (simbol
) dan failure (simbol ![]() ), Bernoulli Trials juga bisa digunakan dalam skenario lain seperti pelemparan dadu. Tinggal menentukan kondisi apa yang dilabeli success. Ambil contoh kita menyebut success jika dalam pelemparan dadu kita mendapat angka enam sehingga peluang success dan failure menjadi seperti ini.
), Bernoulli Trials juga bisa digunakan dalam skenario lain seperti pelemparan dadu. Tinggal menentukan kondisi apa yang dilabeli success. Ambil contoh kita menyebut success jika dalam pelemparan dadu kita mendapat angka enam sehingga peluang success dan failure menjadi seperti ini.
![]()
![]()
Syarat
Jika dirinci, setidaknya ada tiga syarat sebuah percobaan disebut sebagai Bernoulli Trial, yaitu:
- Hanya ada dua kemungkinan hasil (output) percobaan, misal: 1/0, merah/putih, ganjil/genap. Salah satu hasil tersebut kemudian dilabeli sebagai success sedang satunya lagi sebagai failure.
- Tiap hasil percobaan memiliki probabilitas yang tetap, yaitu nilai probabilitas
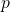 untuk sukses dan nilai probabilitas
untuk sukses dan nilai probabilitas  untuk gagal. Dalam kasus pelemparan koin, probabilitas mendapat kepala selalu
untuk gagal. Dalam kasus pelemparan koin, probabilitas mendapat kepala selalu 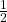 . Saat melempar dadu, peluang mendapat angka 6 selalu
. Saat melempar dadu, peluang mendapat angka 6 selalu 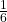 .
. - Tiap percobaan hasilnya independen. Apapun hasil pelemparan koin pertama tidak akan mempengaruhi pelemparan selanjutnya, begitu pula sebaliknya.
Binomial Distribution
Bernoulli Distribution membahas tentang kejadian yang hanya sekali. Bagaimana jika ada serangkaian percobaan yang sama, berulang kali. Seperti melempar dua koin berulang-ulang sampai sebanyak ![]() kali?
kali?
Binomial Distribution adalah distribusi yang dihasilkan dari serangkaian percobaan Bernoulli yang berurutan.
Dalam pelemparan 2 koin sebanyak 2 kali, berapa kemungkinan mendapatkan 4 kepala ![]() ?
?
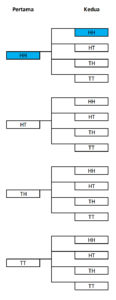
Peluang mendapatkan ![]() adalah
adalah ![]() sehingga peluang mendapatkan
sehingga peluang mendapatkan ![]() adalah
adalah ![]() .
.
![]()
Tantangan ditingkatkan, berapa peluang mendapatkan hanya satu ![]() dalam 2 kali pelemparan 2 koin?
dalam 2 kali pelemparan 2 koin?
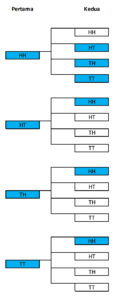
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Formula
Melempar dua kali saja sudah cukup memusingkan. Untungnya Binomial Distribution punya formula untuk menghitung peluang tersebut.
![]()
Dimana:
![]() probabilitas binomial
probabilitas binomial
![]() banyaknya percobaan success
banyaknya percobaan success
![]() banyaknya semua percobaan
banyaknya semua percobaan
![]() nilai probabilitas masing-masing percobaan success
nilai probabilitas masing-masing percobaan success
![]() variabel random yang mengikuti distribusi binomial
variabel random yang mengikuti distribusi binomial
Untuk ![]() dimana
dimana
![]()
adalah binomial coefficient.
Kita coba terapkan formula tersebut pada 4 kepala ![]() .
.
Maka ![]() yaitu 2 kali sukses mendapatkan
yaitu 2 kali sukses mendapatkan ![]() ,
, ![]() adalah 2 kali pelemparan dengan
adalah 2 kali pelemparan dengan ![]() yaitu peluang mendapatkan
yaitu peluang mendapatkan ![]() sehingga perhitungannya menjadi.
sehingga perhitungannya menjadi.
![]()
![]()
![]()
![]()
Lalu untuk kasus 2 kepala ![]() .
.
Maka digunakan ![]() yaitu 1 kali sukses mendapatkan
yaitu 1 kali sukses mendapatkan ![]() ,
, ![]() karena terdapat 2 kali pelemparan dengan
karena terdapat 2 kali pelemparan dengan ![]() yaitu peluang mendapatkan
yaitu peluang mendapatkan ![]() dan perhitungannya menjadi.
dan perhitungannya menjadi.
![]()
![]()
![]()
Jika menggunakan R, berikut hasil dua perhitungan di atas.
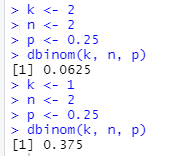
Menggunakan RStudio kita dapat membuat grafik distribusi binomial untuk probabilitas ![]() sebanyak
sebanyak ![]() kali.
kali.
graph <- function(n,p){
x <- dbinom(0:n,size=n,prob=p)
barplot(x,ylim=c(0,0.4),names.arg=0:n,
main=sprintf(paste('Binomial Distribution(n,p) ',n,p,sep=',')))
}
graph(20, 0.25)
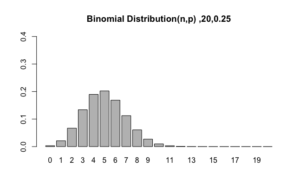
Agak rinci, berikut peluang masing-masing nilai k 0, 4, 5, 6 dan 20.
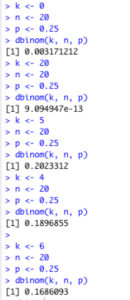
Selain menggunakan perspektif “berapa peluang mendapatkan ![]() ” seperti di atas, rumus tersebut juga dapat digunakan dengan perspektif “berapa peluang mendapatkan angka acak 0, 4, 5, 6 dan 20 jika serangkaian percobaan bernoulli, dengan probabilitas kesuksesan sebesar
” seperti di atas, rumus tersebut juga dapat digunakan dengan perspektif “berapa peluang mendapatkan angka acak 0, 4, 5, 6 dan 20 jika serangkaian percobaan bernoulli, dengan probabilitas kesuksesan sebesar ![]() , dilakukan sebanyak 20 kali“.
, dilakukan sebanyak 20 kali“.
Syarat
Karena Bernoulli Trial memiliki syarat maka Binomial Distribution memiliki syarat yang sama dengan tambahan satu, yaitu jumlah percobaan tetap sebanyak ![]() kali. Sehingga secara lengkap Binomial Distribution membutuhkan empat syarat berikut.
kali. Sehingga secara lengkap Binomial Distribution membutuhkan empat syarat berikut.
- Hanya ada dua kemungkinan hasil (output) pada masing-masing percobaan, misal: 1/0, merah/putih, ganjil/genap.
- Tiap hasil percobaan memiliki probabilitas yang tetap.
- Tiap percobaan hasilnya independen.
- Jumlah percobaan tetap.
Bernoulli Distribution
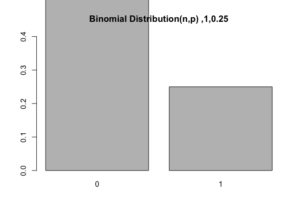
Pada dasarnya Bernoulli Distribution dapat pula dianggap sebagai Binomial Distribution dengan jumlah percobaan sekali (![]() ). Jika langsung diaplikasikan pada R.
). Jika langsung diaplikasikan pada R.

Dengan grafik distribusi seperti ini (tidak mengejutkan).
Lebih Lanjut
https://en.wikipedia.org/wiki/List_of_probability_distributions
https://id.wikipedia.org/wiki/Statistika_inferensi
https://rumusrumus.com/statistika-deskriptif/
http://www.makalah.co.id/2012/10/statistik-inferensial_8934.html
https://www.kompasiana.com/apriancos/56efdbfaa823bd970aee7132/statistik-inferensia-rangkuman-singkat
http://www.en.globalstatistik.com/pengertian-statistik-deskriptif-dan-statistik-inferensial/
https://laelitm.com/statistika-inferensial
https://statmat.id/pengertian-statistik-deskriptif-dan-statistik-inferensia/
http://mathworld.wolfram.com/StatisticalDistribution.html
https://en.wikipedia.org/wiki/Probability_distribution
https://towardsdatascience.com/statistical-distributions-24b5b4ba43cc
https://www.researchgate.net/post/What_are_the_application_inferential_statistics
http://www.statsdata.my.id/2014/06/pengantar-probabilitas.html
https://en.wikipedia.org/wiki/Elementary_event
https://en.wikipedia.org/wiki/Sample_space
https://towardsdatascience.com/statistical-distributions-24b5b4ba43cc
https://en.wikipedia.org/wiki/Probability_distribution
https://statisticsbyjim.com/basics/probability-distributions/
https://www.youtube.com/watch?v=WNgcmn5cXjI
https://www.youtube.com/watch?v=NaDZ0zVTyXQ&list=PL5pdglZEO3NhwZHz5H1hUOqIzGNuNF4_b&index=2
https://towardsdatascience.com/understanding-bernoulli-and-binomial-distributions-a1eef4e0da8f
https://www.youtube.com/watch?v=mOkvzPkWBTc
http://www.math.wichita.edu/history/Topics/probability.html
https://rpubs.com/JanpuHou/294842
Photo by Brett Sayles from Pexels

One Reply to “Statistical Distributions – The Binomial Distribution”