
Measures of Variation
Diskusi statistika deskriptif selanjutnya setelah central tendency adalah mengukur variasi data. Jika pada central tendency yang diukur adalah “apa yang ada di tengah” atau “apa yang paling banyak” maka di bagian ini yang akan dinilai adalah “bagaimana tersebarnya data” atau “jarak dari satu data ke tengah” intinya soal variasi data.
Ada beberapa ukuran yang digunakan: Range, Interquartile Range (IQR), Mean Absolute Deviation, Median Absolute Deviation, Variance dan Standard Deviation.
Kita akan menjelajah sumber data lain yang tak kalah menarik dari data.go.id yaitu data.jakarta.go.id. Dan tak lupa, kita akan menggunakan R Console untuk mencoba konsep-konsep yang kita bahas.
1. Range
Konsep ini sederhana, untuk menentukan range alias jangkauan data maka kita mengurangkan nilai tertinggi dengan nilai terendah.
![]()
Untuk mencoba konsep ini di R, sila unduh data harga bahan pokok di DKI tahun 2018 terlebih dahulu (gunakan ini untuk data Desember).
Kali ini kita akan membiarkan kemalasan menjadi pemandu. Alih-alih mengetik data, kita akan me-load dari berkas csv yang telah kita unduh.
Jika berkas tersebut ada di /home/user/Downloads/Harga-Harian-Bapok-Desember-2018.csv maka kita ketik di R Console.
> goods <- read.csv("/home/user/Downloads/Harga-Harian-Bapok-Desember-2018.csv")
Bila tak ada aral melintang maka di tab environment pada panel kanan atas (panel nomor 3 jika merujuk gambar buruk ini) akan ada data goods yang terdiri dari 723 obs (observations/baris) dan 6 variables.

Jikalau diklik data tersebut maka panel 1 akan menampilkan data goods.
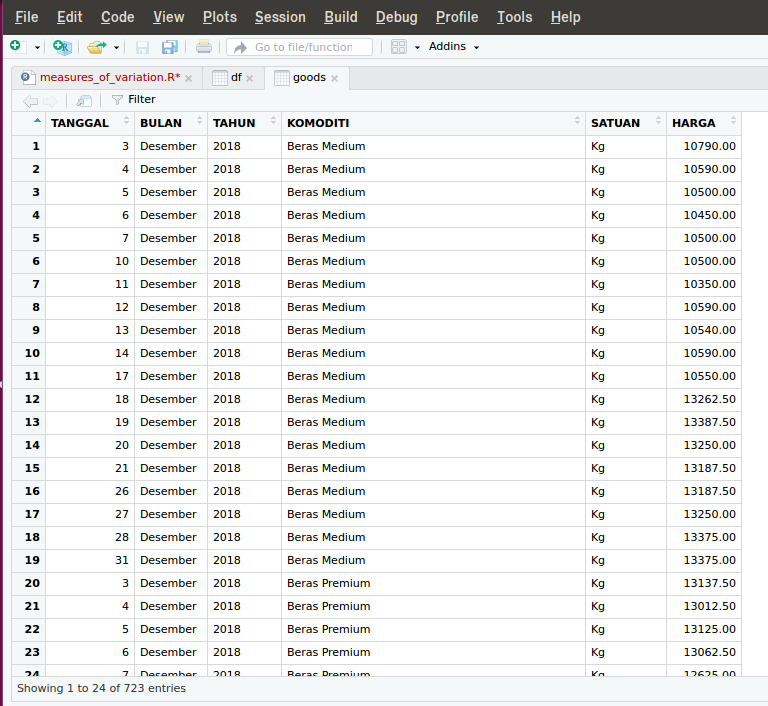
Seperti yang seharusnya, read.csv adalah fungsi dalam paket bawaan R yang digunakan untuk me-load data dari berkas csv. Untuk mengetahui parameter apa saja yang dapat digunakan dalam fungsi ini, sila melihat dokumentasi melalui tab help di panel kanan bawah R Studio.
Dalam pada itu kita hanya akan mengambil harga Beras Medium pada tanggal 3 sampai 31 Desember di baris (observasi) 1-19. Menggunakan R, ada beberapa fungsi yang dapat digunakan untuk mencapai hal tersebut (data subsetting).
> medium_rice1 <- goods[1:19,]
Variabel medium_rice1 diisi data baris 1-19 dari goods. Untuk penulis awalnya agak aneh melihat [1:19,], untuk 1:19 dapat dimengerti, itu berarti baris pertama sampai ke-19. Namun kenapa ada koma lalu tiba-tiba ditutup kurung sikunya? Ternyata kurung siku harus diisi dengan baris dan kolom yang akan diambil, dipisahkan dengan tanda koma. Bila tanpa koma (hanya baris saja yang diisi) maka R akan protes karena tidak terdapat informasi kolom mana yang akan diambil, kita memiliki 6 kolom dalam goods. Jika ada koma meski tanpa angka setelahnya (langsung tutup kurung) maka R menganggap kita ingin mengambil semua kolom.

Sedang bila kita menulis kode dengan tepat maka hasilnya seperti ini.
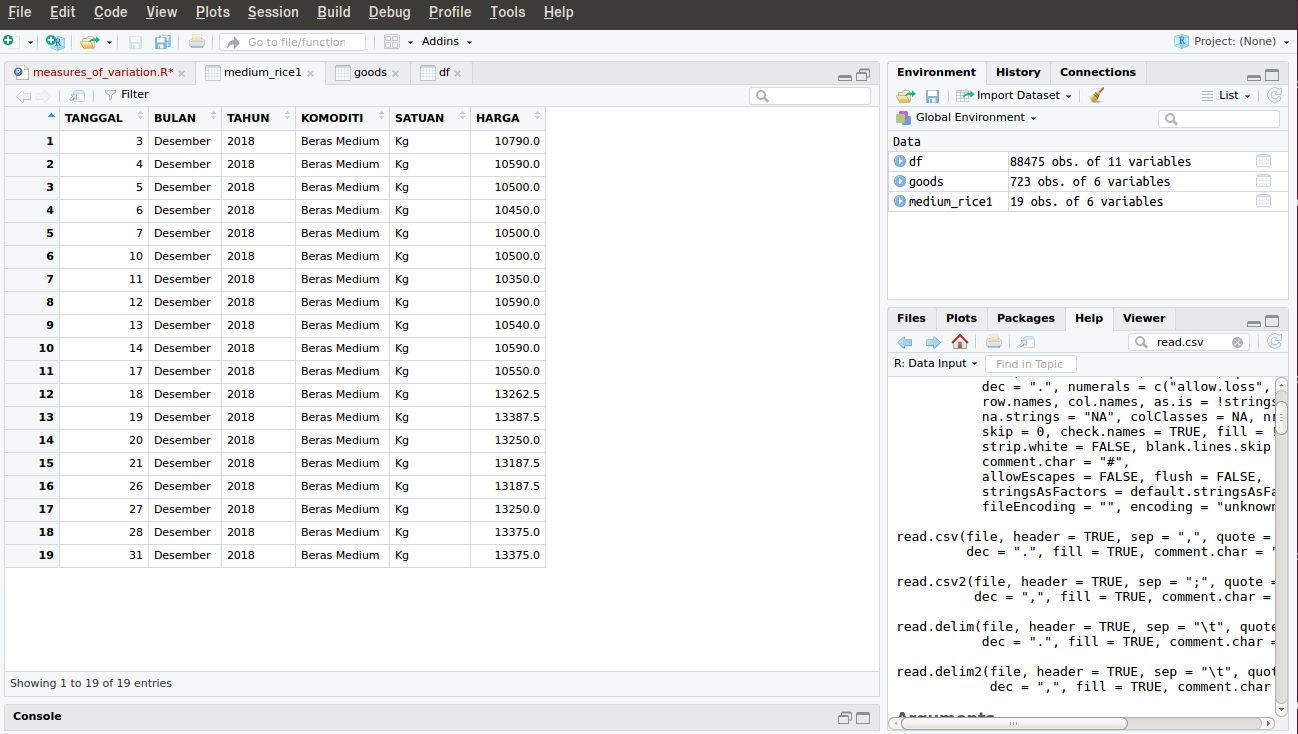
Kode di atas efektif jika kita mengetahui baris mana saja yang akan diambil namun seringnya data tidak datang dalam bentuk yang kita harapkan, entah tidak urut, tidak seragam (terutama penulisan teks) atau bahkan hilang. Kembali ke data bahan pokok kita, secara visual dapat kita tahu bahwa kolom KOMODITI selalu konsisten, Beras Medium. Konsistensi itu dapat kita manfaatkan untuk mengambil data berdasarkan nilai/isi kolom (mem-filter).
> medium_rice2 <- subset(goods, KOMODITI=="Beras Medium")
Jangan sampai terlewat, kita menggunakan 2 sama dengan (KOMODITI==”Beras Medium”) bukan 1 sama dengan, karena 1 sama dengan adalah operator penugasan (assignment operator) sedangkan 2 sama dengan adalah operator pembanding. Hasil kode di atas konsisten dengan kode sebelumnya, karena data telah urut sehingga kode pertama menghasilkan yang sama dengan kode kedua.
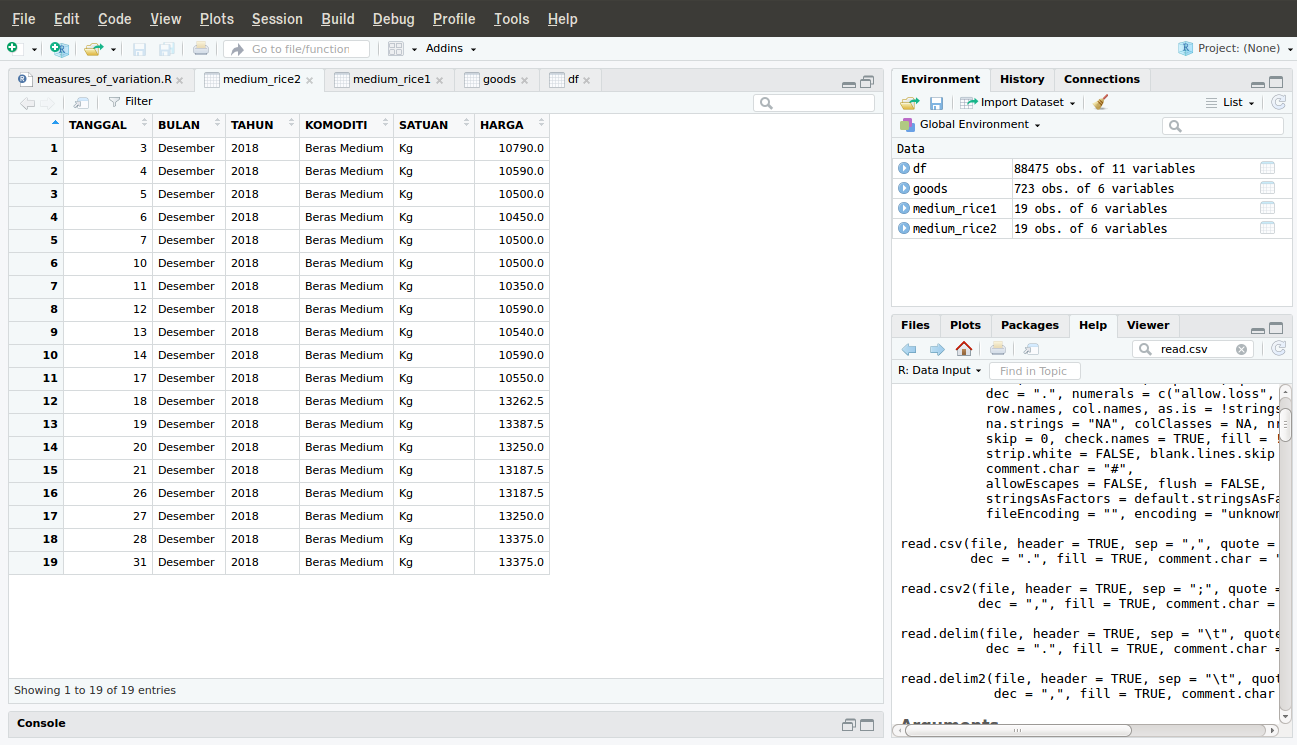
Sebenarnya kita hanya perlu kolom harga, sehingga kita ambil itu saja.
> dummy_data <- medium_rice1$HARGA
Atau bisa juga langsung saat mengambil dari data goods.
> medium_rice_dummy1 <- goods[1:19,c("HARGA")]
> medium_rice_dummy2 <- subset(goods, KOMODITI=="Beras Medium",c("HARGA"))
Hasilnya kurang lebih sama antara dummy_data, medium_rice_dummy1 dan medium_rice_dummy2.
Dan sampailah pada pokok pembahasan, mencari range.
> range(dummy_data) [1] 10350.0 13387.5
Harga beras medium termurah Rp10.350 dan termahal Rp13.387,5. Secara visual dapat pula diidentifikasi nilai maksimum dan minimum dengan mengurutkan data.
> sort(dummy_data) [1] 10350.0 10450.0 10500.0 10500.0 10500.0 10540.0 10550.0 10590.0 10590.0 10590.0 10790.0 13187.5 13187.5 13250.0 [15] 13250.0 13262.5 13375.0 13375.0 13387.5
Jika ingin mendapatkan Range seperti rumus di awal maka kode ini dapat digunakan.
> range(dummy_data)[2] - range(dummy_data)[1] [1] 3037.5
Dalam penggunaan range perlu diperhatikan setidaknya dua hal.
- Sensitif terhadap nilai ekstrim.
- Karena hanya menggunakan dua angka maka range tidak benar-benar mencerminkan variasi data.
2. Interquartile Range (IQR)
Kita mulai dengan quantile dulu, apakah itu? Quantile adalah nilai/jumlah yang membagi data menjadi bagian yang sama banyaknya. Beberapa jenis quantile adalah.
- Quartile/kuartil, membagi data menjadi 4
- Decile/Desil, membagi data menjadi 10
- Percentile/Persentile, membagi data menjadi 100
Kembali ke quartile yang dalam bahasa kita diterjemahkan sebagai kuartil. Jika data kita bagi menjadi empat, maka perlu digaris sebanyak tiga kali, Q1, Q2 dan Q3.
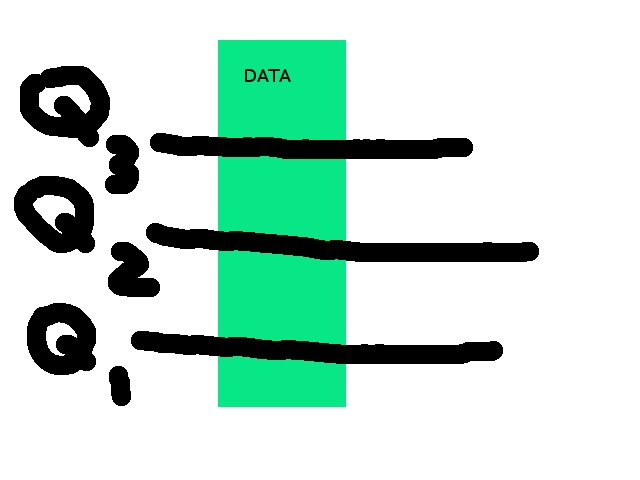
Q2 adalah median, nilai yang berada di tengah-tengah data, alias posisi di 50%. Sehingga Q1 adalah posisi ke-25 dan Q3 posisi ke-75.
R memiliki fungsi quantile yang dapat digunakan untuk mendapatkan nilai kuartil ini.
> dummy_q <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) > quantile(dummy_q, probs = c(.25)) 25% 3.25
Untuk mendapatkan Q1 dan Q3 maka dapat digunakan kode ini.
> quantile(dummy_q, probs = c(.25, .75)) 25% 75% 3.25 7.75
IQR didapatkan dari Q3 – Q1.
> quantile(dummy_q, probs = c(.25, .75))[2] - quantile(dummy_q, probs = c(.25, .75))[1] 75% 4.5
Atau dengan fungsi bawaan R yang membuat kita tidak perlu mengetik banyak.
> IQR(dummy_q) [1] 4.5
IQR dapat diinterpretasikan sebagai jarak/jangkauan (range) area tengah data. Jika menggunakan distribusi normal maka mayoritas data akan berada dalam range IQR tersebut.
3. Mean Absolute Deviation
Deviasi adalah jarak. Jarak apa ke apa? Jarak dari tiap-tiap data ke Mean (nilai rata-rata data). Jarak tersebut dibuat menjadi absolut (dipositifkan). Mean Absolute Deviation dirumuskan menjadi.
![Rendered by QuickLaTeX.com \[ \text{Mean Absolute Deviation(X)} = \frac{1}{N}\sum_{i=1}^N |X_i - \bar{X}| \]](https://basangdata.com/wp-content/ql-cache/quicklatex.com-482d1b6637ac526ece08fb0319b67d5c_l3.png)
Menggunakan contoh dummy_q di atas, kita mendapatkan data seperti ini.
| Mean ( |
Deviation ( |
Absolute Deviation | ||
|---|---|---|---|---|
| 1 | 1 | 5.5 | -4.5 | 4.5 |
| 2 | 2 | 5.5 | -3.5 | 3.5 |
| 3 | 3 | 5.5 | -2.5 | 2.5 |
| 4 | 4 | 5.5 | -1.5 | 1.5 |
| 5 | 5 | 5.5 | -0.5 | 0.5 |
| 6 | 6 | 5.5 | 0.5 | 0.5 |
| 7 | 7 | 5.5 | 1.5 | 1.5 |
| 8 | 8 | 5.5 | 2.5 | 2.5 |
| 9 | 9 | 5.5 | 3.5 | 3.5 |
| 10 | 10 | 5.5 | 4.5 | 4.5 |
| 55 | 0 | 25 |
Dimana ![]() adalah masing-masing angka, dari 1 sampai 10. Jumlah data, N, adalah 10. Mean
adalah masing-masing angka, dari 1 sampai 10. Jumlah data, N, adalah 10. Mean ![]() adalah
adalah ![]() .
.
Deviasi (jarak) adalah masing-masing angka dikurangi mean, hasilnya dapat berupa positif dan negatif. Karena akan dijumlahkan maka deviasi tersebut perlu diabsolutkan (dijadikan positif), jika tidak absolut maka hasil penjumlahan menjadi tidak mewakili rata-rata jarak masing-masing data. Dalam contoh di atas, hasil penjumlahan deviasi adalah nol.
Dengan angka absolut maka penjumlahan menjadi bermakna, senilai 25 dan nilai Mean Absolute Deviation adalah.
![Rendered by QuickLaTeX.com \[ Mean Absolute Deviation(dummyq) = \frac{1}{10}\sum_{i=1}^{10} |X_i - \bar{X}| = \frac{25}{10} = 2.5 \]](https://basangdata.com/wp-content/ql-cache/quicklatex.com-235e75b8414c1adcd8253f605ac5be82_l3.png)
Dari ilustrasi perhitungan di atas, secara intuitif kita dapat menyimpulkan jika Mean Absolute Deviation menunjukkan umumnya (tipikal) jarak data dengan nilai mean.
Pada R, kita dapat menghitung Mean Absolute Deviation dengan fungsi mad dengan contoh kode.
> dummy_q <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) > mad(dummy_q, mean(dummy_q), 1) [1] 2.5
Atau menggunakan kode seperti di sini.
> mean(abs(dummy_q - mean(dummy_q))) [1] 2.5
4. Median Absolute Deviation
Median Absolute Deviation, disingkat MAD, merupakan nilai tengah dari deviasi antara masing-masing data dan median data ![]() . Deviasi di sini berbeda dengan deviasi sebelumnya yang mengurangkan antara masing-masing data dengan mean data
. Deviasi di sini berbeda dengan deviasi sebelumnya yang mengurangkan antara masing-masing data dengan mean data ![]() .
.
![]()
Sebagai ilustrasi, kita akan menggunakan data halaman wikipedia mengenai MAD.
| Median ( |
Absolute Deviations (| |
||
|---|---|---|---|
| 1 | 1 | 2 | 1 |
| 2 | 1 | 2 | 1 |
| 3 | 2 | 2 | 0 |
| 4 | 2 | 2 | 0 |
| 5 | 4 | 2 | 2 |
| 6 | 6 | 2 | 4 |
| 7 | 9 | 2 | 7 |
![]()
Jadi MAD adalah 1.
> dummy_mad <- c(1, 1, 0, 0, 2, 4, 7) > mad(dummy_mad, median(dummy_mad), 1) [1] 1
Atau.
> median(abs(dummy_mad - median(dummy_mad))) [1] 1
Guna MAD adalah mengukur sebaran data, mirip dengan standard deviasi (yang akan dibahas nanti), namun lebih tahan dengan outliers, dengan alasan yang kurang lebih sama yang diterangkan di bagian intermezzo tulisan sebelumnya.
Untuk artikel lebih serius mengenai 2 MAD ini, silahkan ke sini, dapat didownload uga lo.
5. Variance
Mirip dengan Mean Absolute Deviation namun alih-alih diabsolutkan, deviasi dikuadratkan untuk menghindari nilai negatif.
![Rendered by QuickLaTeX.com \[ Var(X) = \frac{1}{N}\sum_{i=1}^N (X_i - \bar{X})^2 \]](https://basangdata.com/wp-content/ql-cache/quicklatex.com-a1718f385f0e51bb09b630e9e426adf0_l3.png)
Kembali menggunakan contoh dummy_q di atas, dimodifikasi menjadi seperti ini.
| Mean ( |
Deviation ( |
Squared Deviations |
||
|---|---|---|---|---|
| 1 | 1 | 5.5 | -4.5 | 20.25 |
| 2 | 2 | 5.5 | -3.5 | 12.25 |
| 3 | 3 | 5.5 | -2.5 | 6.25 |
| 4 | 4 | 5.5 | -1.5 | 2.25 |
| 5 | 5 | 5.5 | -0.5 | 0.25 |
| 6 | 6 | 5.5 | 0.5 | 0.25 |
| 7 | 7 | 5.5 | 1.5 | 2.25 |
| 8 | 8 | 5.5 | 2.5 | 6.25 |
| 9 | 9 | 5.5 | 3.5 | 12.25 |
| 10 | 10 | 5.5 | 4.5 | 20.25 |
| 55 | 0 | 82.5 |
Maka variance adalah.
![]()
Kita uji menggunakan R.
> var(dummy_q) [1] 9.166667
APA!!! (zoom in, zoom out)
Hmm… Kita uji dulu dengan perhitungan manual.
> mean((dummy_q - mean(dummy_q))^2) [1] 8.25
Kenapa fungsi bawaan R menghasilkan angka 9.16 alih-alih 8.25? Ternyata karena fungsi tersebut menggunakan rumus yang sedikit berbeda. Pembagi yang digunakan adalah ![]() bukan
bukan ![]() seperti yang kita gunakan.
seperti yang kita gunakan.
![Rendered by QuickLaTeX.com \[ Var(X) = \frac{1}{N-1}\sum_{i=1}^N (X_i - \bar{X})^2 \]](https://basangdata.com/wp-content/ql-cache/quicklatex.com-ea2192d6eb4cde87628e1bd14ca6d42c_l3.png)
Pembagi tersebut, ![]() adalah Bessel’s Correction yang diterapkan pada sample variance
adalah Bessel’s Correction yang diterapkan pada sample variance ![]() sedangkan
sedangkan ![]() sebelumnya adalah pembagi pada population variance
sebelumnya adalah pembagi pada population variance ![]() .
.
![Rendered by QuickLaTeX.com \[ \sigma^2 = \frac{1}{N}\sum_{i=1}^N (X_i - \bar{X})^2 \]](https://basangdata.com/wp-content/ql-cache/quicklatex.com-63064fc6407d48682167922519efc2b1_l3.png)
![Rendered by QuickLaTeX.com \[ s^2 = \frac{1}{N-1}\sum_{i=1}^N (X_i - \bar{X})^2 \]](https://basangdata.com/wp-content/ql-cache/quicklatex.com-dc64cf0534bc55b6975df6ed92e69b5d_l3.png)
Berhubungan dengan matematika memang tidak pernah mudah, sekedar menjelaskan beda ![]() dan
dan ![]() saja butuh banyak pengetahuan, populasi lah, bias lah dan banyak ubo rampe lainnya. Karena itu kita simpan dulu penjelasan soal itu, di masa depan kita akan mereviu lagi pemahaman kita, untuk sementara kita terima saja
saja butuh banyak pengetahuan, populasi lah, bias lah dan banyak ubo rampe lainnya. Karena itu kita simpan dulu penjelasan soal itu, di masa depan kita akan mereviu lagi pemahaman kita, untuk sementara kita terima saja ![]() sebagai pembagi variance.
sebagai pembagi variance.
> sum((dummy_q - mean(dummy_q))^2)/9 [1] 9.166667
Up to this time sejujurnya penulis masih tak paham guna variance ini, terutama karena pangkat dua yang membuat nilainya tidak setara dengan data.
6. Standard Deviation
Lanjutan dari variance, supaya mendapatkan nilai yang setara dengan data, maka pangkat dua diakar pangkat dua (ba dum tss). Hasilnya disebut Standar Deviasi.
Karena telah terlanjur mengenalkan dua jenis variance, sample variance dan population variance maka terdapat dua jenis standar deviasi.
![Rendered by QuickLaTeX.com \[ \hat{\sigma} = \sqrt{\frac{1}{N}\sum_{i=1}^N (X_i - \bar{X})^2} \]](https://basangdata.com/wp-content/ql-cache/quicklatex.com-08ddff5bb10a7b9ae5094a5ccc46dfc1_l3.png)
Untuk standar deviasi populasi, dan.
![Rendered by QuickLaTeX.com \[ s = \sqrt{\frac{1}{N-1}\sum_{i=1}^N (X_i - \bar{X})^2} \]](https://basangdata.com/wp-content/ql-cache/quicklatex.com-efb1d2193b3f0317f0cc0764b2dc4723_l3.png)
Untuk standar deviasi sampel.
Untuk menginterpretasikan (menerjemahkan) standar deviasi kita sederhanakan saja, menurut ini standar deviasi menunjukkan bagaimana data terkonsentrasi di sekitar nilai rata-rata, makin besar standar deviasi berarti secara umum data tersebar jauh dari nilai rata-rata, standar deviasi kecil berarti data terkonsentrasi di tengah-tengah.
Menggunakan distribusi normal, akan dibahas nanti mengenai distribusi, kita akan menemukan bahwa mayoritas data (68,27%) akan berada di satu standar deviasi (mean kurang satu dan mean tambah satu).
Di R mendapatkan standar deviasi mudah sekali.
> sd(dummy_q) [1] 3.02765
Bisa kita kira-kira sendiri, tiga koma sekian di atas adalah akar (pangkat dua) dari nilai variance sembilan koma sekian, sesuai perhitungan variance di bagian sebelumnya.
Salam.
Lebih Lanjut:
- https://blog.ub.ac.id/rinaldomakoto/2012/03/22/ukuran-kuartil/
- https://www.thoughtco.com/what-is-the-mean-absolute-deviation-4120569
- https://mathbits.com/MathBits/TISection/Statistics1/MAD.html
- https://www.mathsisfun.com/data/mean-deviation.html
- https://stat.ethz.ch/R-manual/R-devel/library/stats/html/mad.html
- https://stats.stackexchange.com/questions/17890/what-is-the-difference-between-n-and-n-1-in-calculating-population-variance
- https://stats.stackexchange.com/questions/198452/why-sample-variance-has-has-n-1-in-the-denominator
- https://stats.stackexchange.com/questions/47728/what-is-the-difference-between-an-estimator-and-a-statistic
- https://stats.stackexchange.com/questions/3931/intuitive-explanation-for-dividing-by-n-1-when-calculating-standard-deviation
- https://courses.lumenlearning.com/boundless-statistics/chapter/describing-variability/
- https://www.dummies.com/education/math/statistics/how-to-interpret-standard-deviation-in-a-statistical-data-set/

One Reply to “Measures of Variation”