
Menggunakan Binomial Distribution
Kemenyan sebesar lutut jika tiada dibakar manakan berbau. Tahu apa itu Binomial Distribution adalah hal yang baik, tapi ilmu yang tak diamalkan, apa gunanya?
Latar Belakang
Selama bisa memenuhi empat rukun yaitu:
- hanya memiliki dua kemungkinan;
- tiap hasil percobaan berprobabilitas tetap;
- tiap percobaan hasilnya independen; dan
- banyaknya percobaan tetap
maka kita dapat menggunakan rumus Binomial Distribution dalam berbagai skenario.
Formula
Sebagai pengingat, berikut formula Binomial Distribution.
![]()
Dimana:
![]() probabilitas binomial
probabilitas binomial
![]() banyaknya percobaan success
banyaknya percobaan success
![]() banyaknya semua percobaan
banyaknya semua percobaan
![]() nilai probabilitas masing-masing percobaan success
nilai probabilitas masing-masing percobaan success
![]() variabel random yang mengikuti distribusi binomial
variabel random yang mengikuti distribusi binomial
Untuk ![]()
Penggunaan
Test Pack
Saat membahas mengenai Bayes ada bahasan mengenai penggunaan test pack berakurasi 99%, yang kurang lebih seperti di bawah ini.
Jika memilih sembarang wanita pada tahun 2016 kemudian menguji dengan test pack dan hasilnya positif, ternyata kemungkinan wanita tersebut benar-benar hamil adalah 81,12%, alih-alih 99% sesuai akurasi test pack.
Kita akan mendaur ulang studi kasus tersebut.
Tahun 2016
Menurut Kementerian Kesehatan pada tahun 2016 ada:
- wanita sejumlah 128.716.296 jiwa; dan
- diantaranya sejumlah 5.354.594 jiwa, 4,16% dari total jumlah wanita, hamil.
Jika disederhanakan, proporsi wanita hamil adalah 4% sedangkan 96% tidak hamil.
Sampel 1.000 Wanita
Untuk memudahkan anggap saja kita memiliki sampel sebanyak 1.000 wanita, terdiri dari 40 orang hamil dan 960 tidak hamil.
Jika menggunakan test pack dengan akurasi 99% artinya ada kemungkinan kesalahan 1%. Jika 1% tersebut dikalikan dengan 960, maka terdapat (![]() , dibulatkan ke bawah menjadi) 9 wanita tidak hamil yang salah dideteksi (False Positive).
, dibulatkan ke bawah menjadi) 9 wanita tidak hamil yang salah dideteksi (False Positive).
Spreadsheet
Umumnya aplikasi spreadsheet, seperti Microsoft Excel, Google Sheets dan lainnya, memiliki formula untuk menghitung Binomial Distribution. Jika menggunakan Excel maupun Sheets, formula di bawah ini dapat digunakan.
=BINOM.DIST(k, n, p, cumulative)
Dimana:
![]() banyaknya percobaan success
banyaknya percobaan success
![]() banyaknya semua percobaan
banyaknya semua percobaan
![]() nilai probabilitas masing-masing percobaan success
nilai probabilitas masing-masing percobaan success
![]() berisi TRUE atau FALSE, jika TRUE maka nilai kumulatif (sampai dengan) akan ditampilkan, jika FALSE maka hanya nilai probabilitas k yang ditampilkan
berisi TRUE atau FALSE, jika TRUE maka nilai kumulatif (sampai dengan) akan ditampilkan, jika FALSE maka hanya nilai probabilitas k yang ditampilkan
Tentu saja kita tetap dapat membuat sendiri formula yang menghasilkan nilai probabilitas k.
Bernoulli Trial
Karena telah dibantu spreadsheet, kita bisa dengan cepat mendapatkan nilai probabilitas untuk masing-masing percobaan sukses alias ![]() .
.
Kita akan menghitung dari 960 wanita tidak hamil, berapa kemungkinan mendapatkan 0 sampai 960 wanita yang salah dideteksi sebagai hamil.
Sehingga ![]() ,
, ![]() dan
dan ![]() .
.
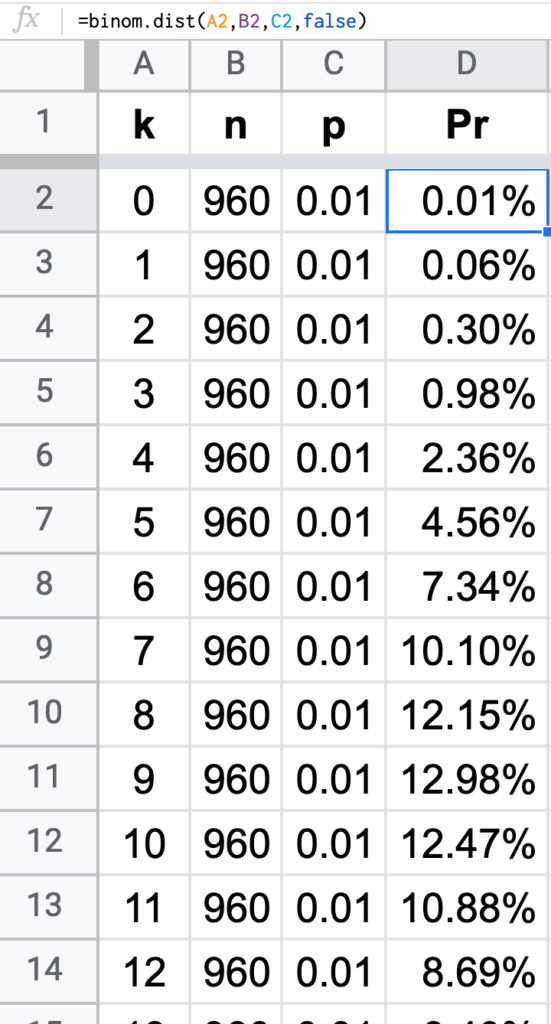
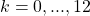
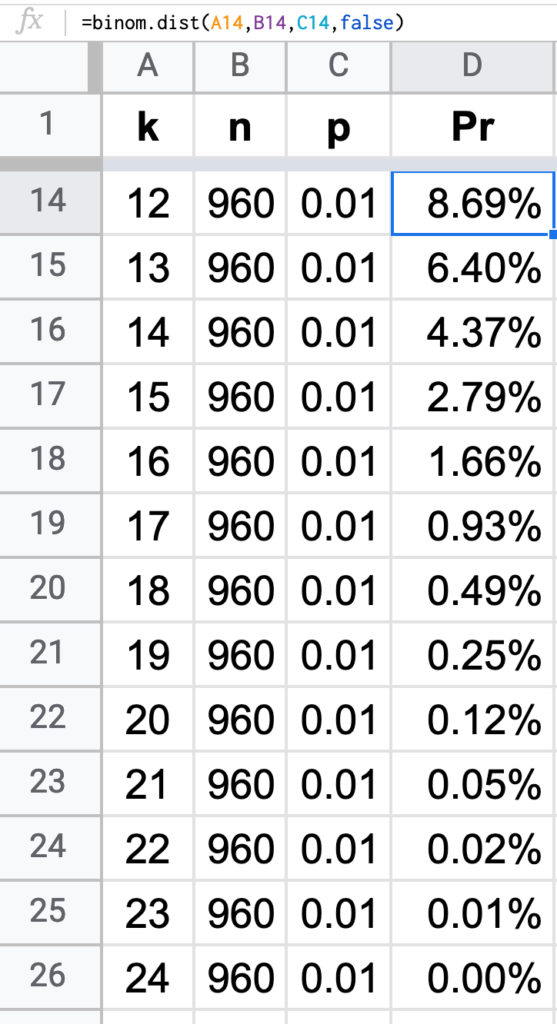
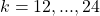
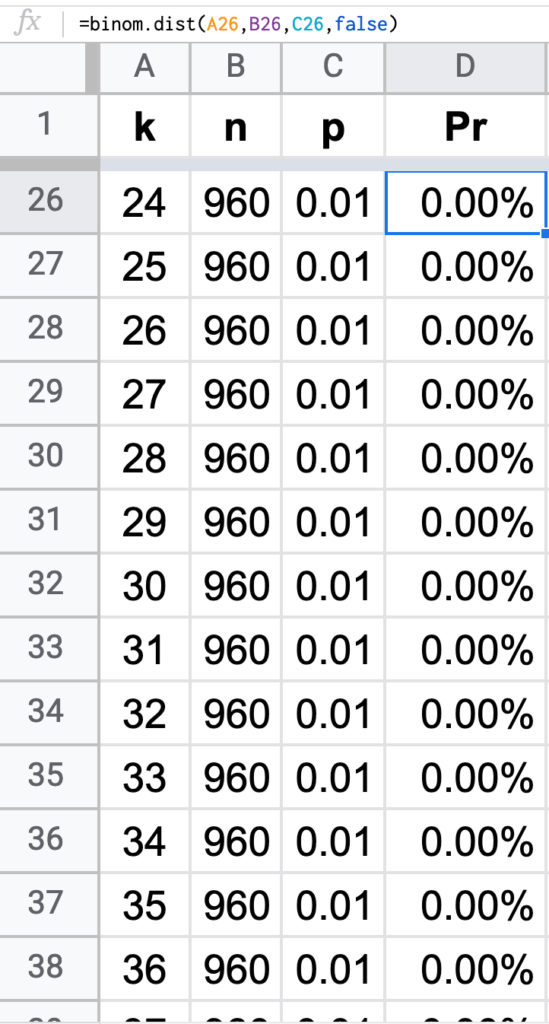
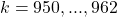
Probabilitas mendapatkan 0 wanita tidak hamil yang dideteksi hamil, sebesar 0,01%. Probabilitas mendapatkan 1 wanita sebesar 0,06%, meningkat.
Peningkatan tersebut konsisten hingga nilai ![]() . Lalu turun mulai
. Lalu turun mulai ![]() hingga
hingga ![]() (jika
(jika ![]() perhitungan bermasalah karena faktorial angka negatif tidak dapat diproses).
perhitungan bermasalah karena faktorial angka negatif tidak dapat diproses).
Untuk lebih memudahkan mencerna data, berikut grafik yang dihasilkan dari Bernoulli Process di atas, ditampilkan hanya sampai ![]() .
.
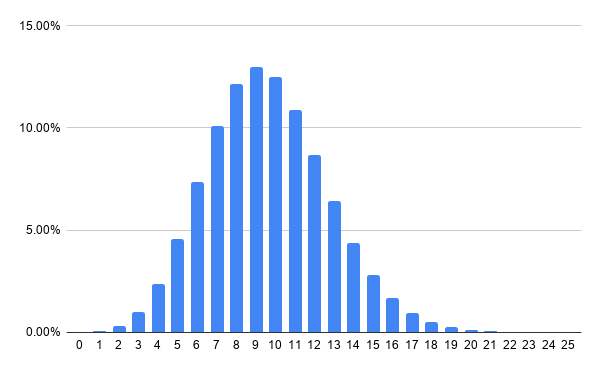
Probabilitas tertinggi, 12,8% terjadi saat
. Hal tersebut memperkuat pernyataan produsen test pack bahwa terdapat kemungkinan salah sebanyak 1%, yang jika diaplikasikan pada 1.000 sampel maka ada 9 False Positive.
Probabilitas saat ![]() , yang tidak bernilai 0 (atau mendekati 0), mengamini temuan Bayes bahwa ada kemungkinan test pack tersebut menghasilkan
, yang tidak bernilai 0 (atau mendekati 0), mengamini temuan Bayes bahwa ada kemungkinan test pack tersebut menghasilkan ![]() False Positive.
False Positive.
Probabilitas yang disediakan oleh Bayes tepatnya seperti ini.
![]()
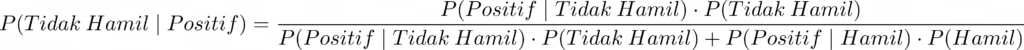
![]()
![]()
Jalur Dua Arah
Sebuah penyelenggara webinar memiliki data peserta dimana ![]() diantaranya adalah laki-laki. Jika dipilih secara acak 6 peserta, berapa kemungkinan 4 diantaranya adalah laki-laki?
diantaranya adalah laki-laki. Jika dipilih secara acak 6 peserta, berapa kemungkinan 4 diantaranya adalah laki-laki?
Jalur Langsung
Umumnya kita akan langsung menerjemahkan menjadi seperti ini.
![]()
![]()
![]()
Sehingga.
![]()
![]()
![]()
Satu Kurang p
Kita ubah sedikit cara pandang persoalan di atas. Jika 4 dari 6 orang yang dipilih secara acak adalah laki-laki, maka 2 diantaranya adalah perempuan.
Ini memanfaatkan salah satu syarat Binomial Distribution, “banyaknya percobaan tetap”.
Lalu jika kita ubah label success menjadi mendapatkan perempuan dari 6 orang yang dipilih secara acak, maka kita memerlukan nilai ![]() yang baru. Untungnya,
yang baru. Untungnya,
salah satu rukun Binomial Distribution adalah tiap percobaan hanya memiliki dua kemungkinan, yang diberi label success dan failure.
Sebagai akibatnya, probabilitas failure adalah ![]() .
.
![]()
![]()
Jika kita gunakan situasi di atas, ![]() maka
maka ![]() . Nilai
. Nilai ![]() inilah yang akan menjadi
inilah yang akan menjadi ![]() yang baru. Sehingga kita dapat mendefinisikan sebagai berikut.
yang baru. Sehingga kita dapat mendefinisikan sebagai berikut.
![]()
![]()
![]()
Kemudian perhitungan menjadi seperti ini.
![]()
![]()
![]()
Hasilnya sama persis dengan perhitungan sebelumnya.
Referensi
Cover Photo by Priscilla Du Preez on Unsplash
