Statistical Distribution – Normal Distribution
Apa itu normal? Apakah (data) kita normal? Apakah menjadi normal itu perlu?
Pertanyaan pembuka tadi mungkin terlalu filosofis (baca: berlebihan).
Fenomena Lazim
Mayoritas artikel mengenai Normal Distribution menyatakan fenomena itu ada di mana-mana, tinggi badan, tekanan darah, dan banyak lainnya.
Namun lebih menyenangkan jika kita dapat membuktikannya sendiri, ye kan?
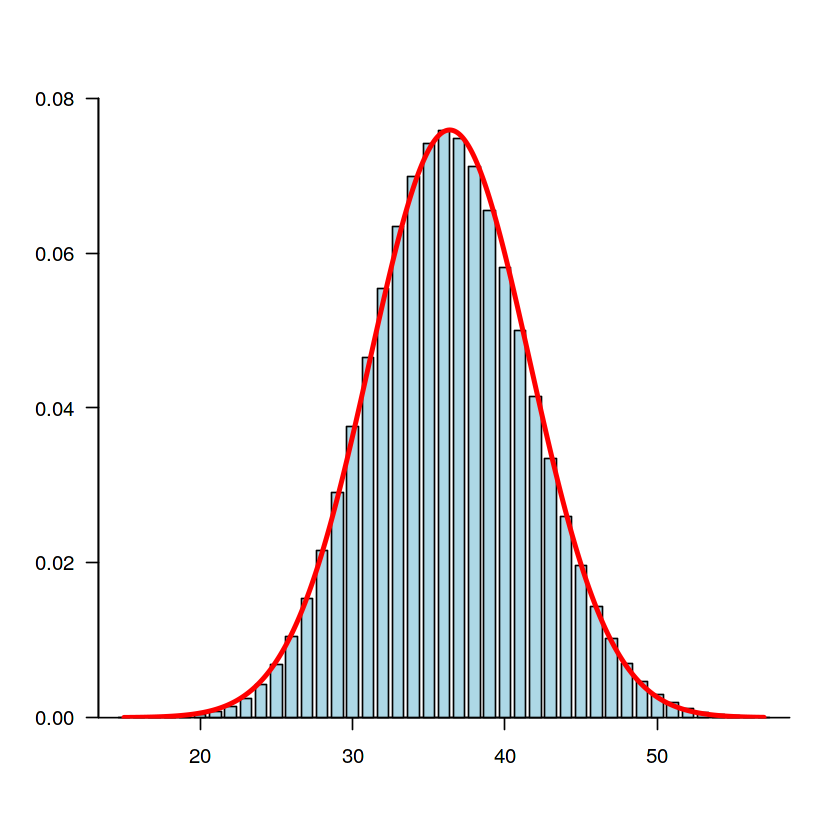
Paling mudah mengenali Normal Distribution adalah melalui grafik yang dihasilkan, yaitu menyerupai lonceng.
Yang entah kenapa selalu ingat Iron Throne dari GOT, jika ketemu barchart seperti di atas.
Kita akan menguji klaim “Normal Distribution ada di mana-mana” menggunakan metode primitif, yaitu apakah sembarang data yang ditemukan menghasilkan lonceng juga, atau setidaknya mirip.
Umur, tinggi, tekanan darah dan nilai ujian adalah data yang “katanya” mengikuti pola lonceng à la Normal Distribution. Kita cari yang memuat empat jenis data tadi.
Kaggle
Menyediakan data dan notebook online dalam satu tempat sehingga cocok digunakan untuk proyek “pengujian klaim” kita.
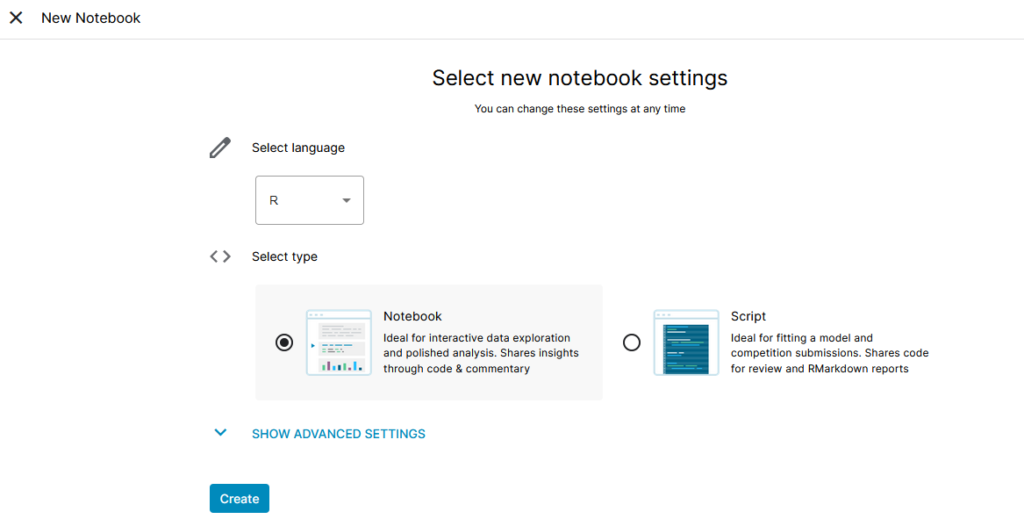
Untuk membuat notebook (atau kadang disebut sebagai kernel) di Kaggle kita dapat menggunakan menu Notebooks > New Notebook.
Cardiovascular Disease dataset
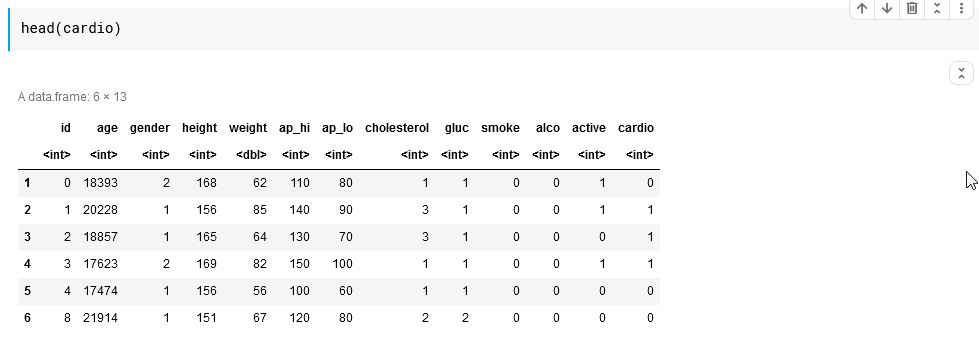
Data ini memuat 70.000 datum pasien, memuat antara lain umur, tinggi, berat, tekanan darah sistolik dan diastolik, kolesterol dan beberapa parameter lainnya.
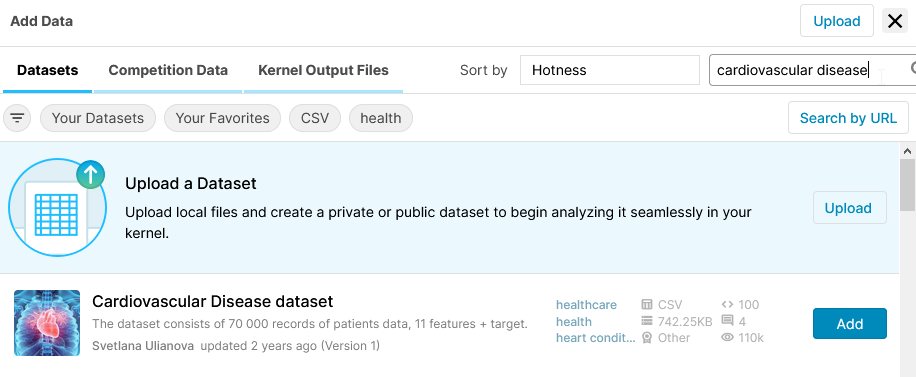
Untuk menambahkan data pada notebook, gunakan menu Add data kemudian ketik nama data yang akan digunakan, klik Add pada data yang dipilih.
Data akan tampil di sebelah kanan. Untuk menggunakan data dalam notebook (dalam hal ini R) klik Copy file path lalu pakai dalam script.
cardio <- read.csv("../input/cardiovascular-disease-dataset/cardio_train.csv", sep=";")
Umur
Dataset ini menggunakan hari sebagai satuan umur, karena itu perlu dibuat sebuah kolom baru berisi umur dalam satuan tahun. Lalu kemudian data ditampilkan dalam bentuk barchart.
library(tidyverse)
cardio$age_y <- round(cardio$age/365, digits=0)
datum <- cardio[c('age_y')]
ggplot(datum, aes(x=age_y)) +
geom_histogram(mapping=aes(y=..density..), fill="steelblue", colour="black", binwidth=1) +
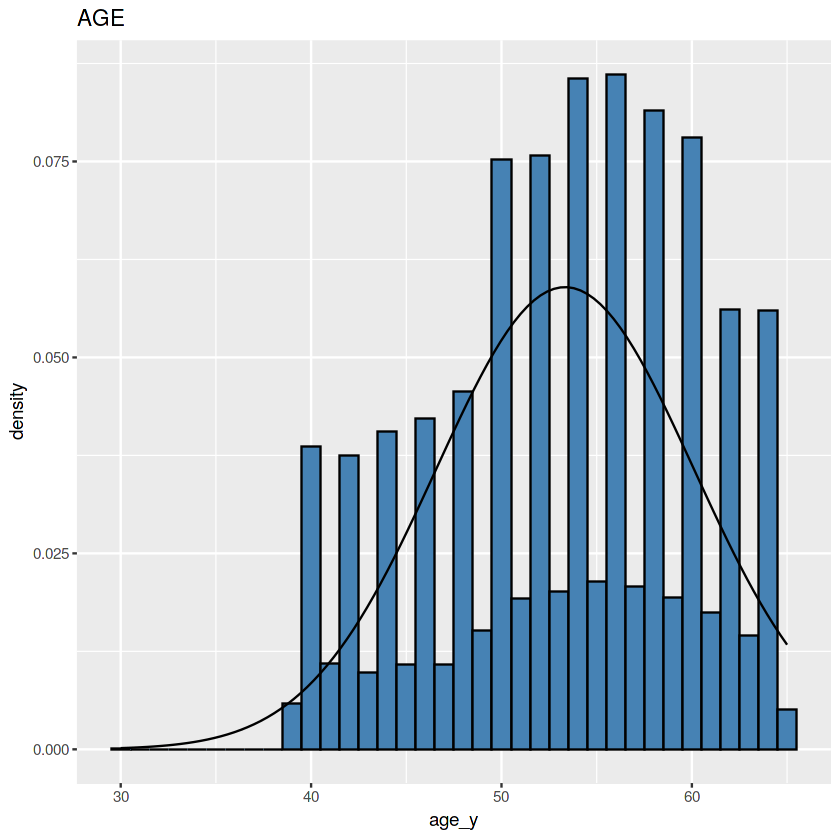
ggtitle("AGE") +
stat_function(fun=dnorm, args=list(mean=mean(datum$age_y), sd=sd(datum$age_y)))
Tidak terlihat seperti lonceng, tapi memang ada bagian “tengah” yang lebih tinggi ketimbang sekelilingnya.
Tinggi
datum <- cardio[c('height')]
ggplot(datum, aes(x=height)) +
geom_histogram(mapping=aes(y=..density..), fill="steelblue", colour="black", binwidth=3) +
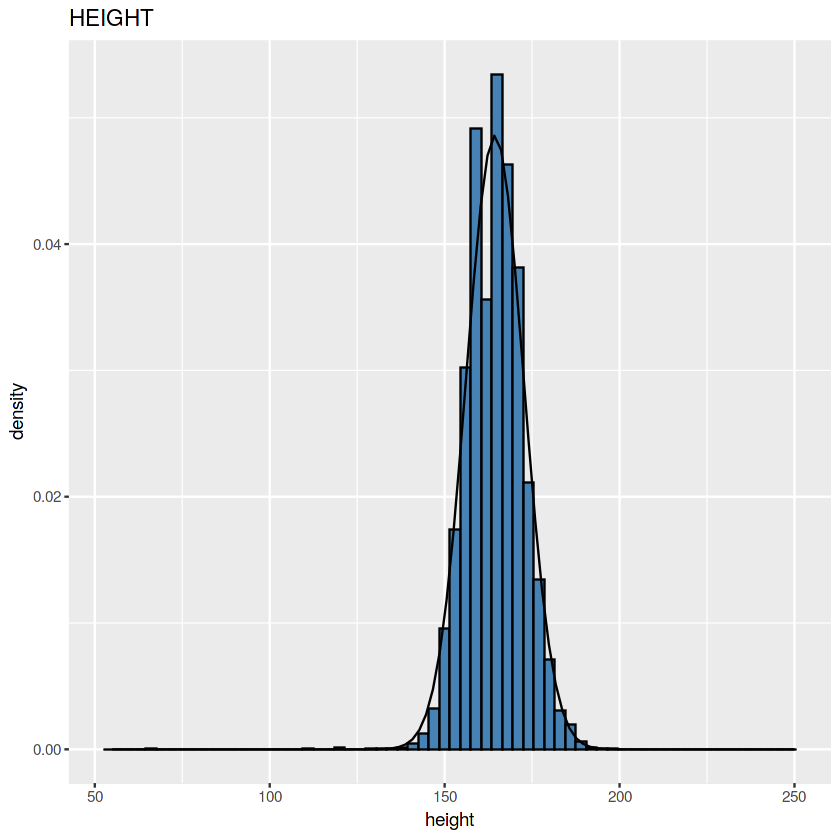
ggtitle("HEIGHT") +
stat_function(fun=dnorm, args=list(mean=mean(datum$height), sd=sd(datum$height)))
Kalo ini emang cukup mirip dengan lonceng.
Tekanan Darah
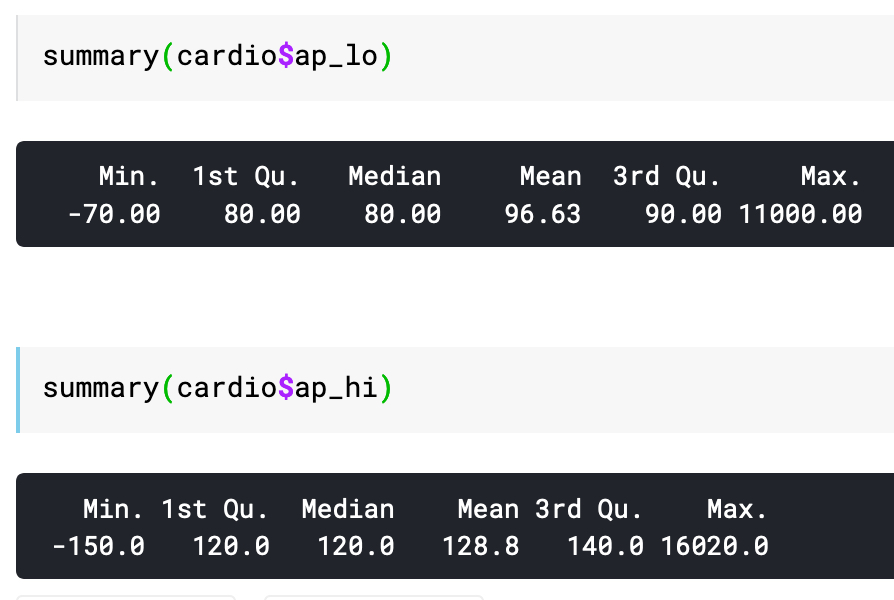
Dataset ini memiliki data tekanan darah sistolik (ap_hi) dan diastolik (ap_hi) namun, seperti umumnya data di dunia nyata, data tersebut masih belum bersih.
Seperti terlihat pada gambar di bawah ini, tekanan darah sistolik terendah adalah -150 dan tertinggi 16.020. Sedang tekanan darah diastolik ada pada rentang -70 sampai 11.000.
Tidak perlu ikut Nusantara Sehat untuk ragu dengan data tersebut. Pilihan yang ada adalah membersihkan data atau menggunakan dataset lain.
Pilihan yang mudah.
Heart Disease UCI
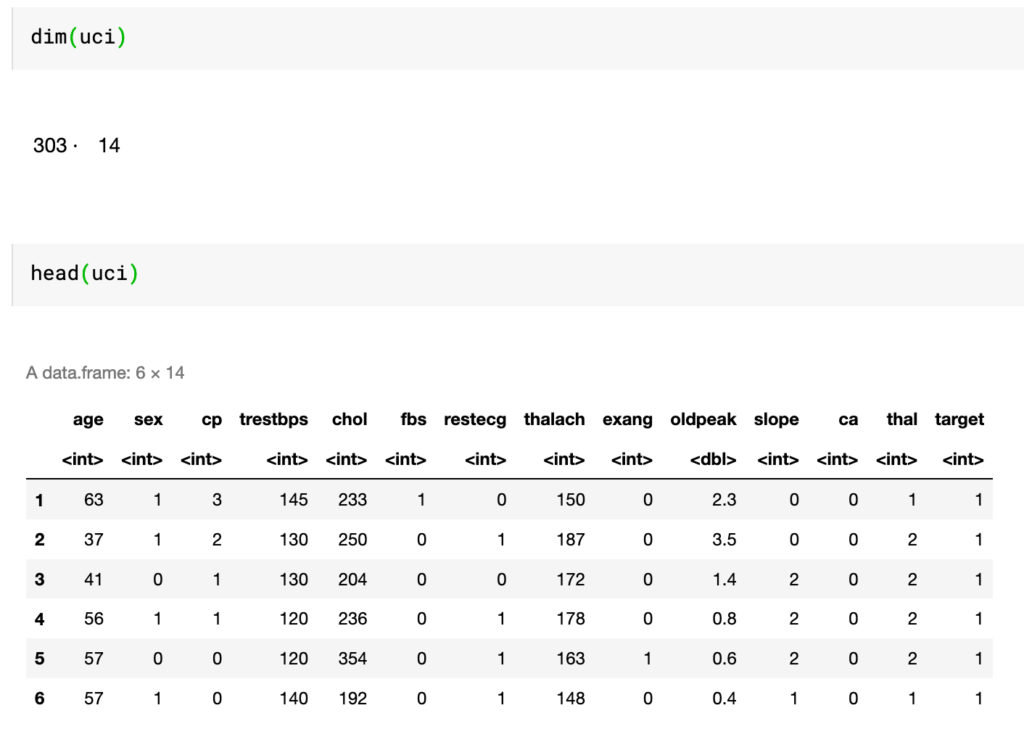
Data UCI ini terdiri dari 303 baris dengan kolom antara lain umur, tekanan darah, gula darah puasa dan lainnya.
uci <- read.csv("../input/heart-disease-uci/heart.csv")
Umur
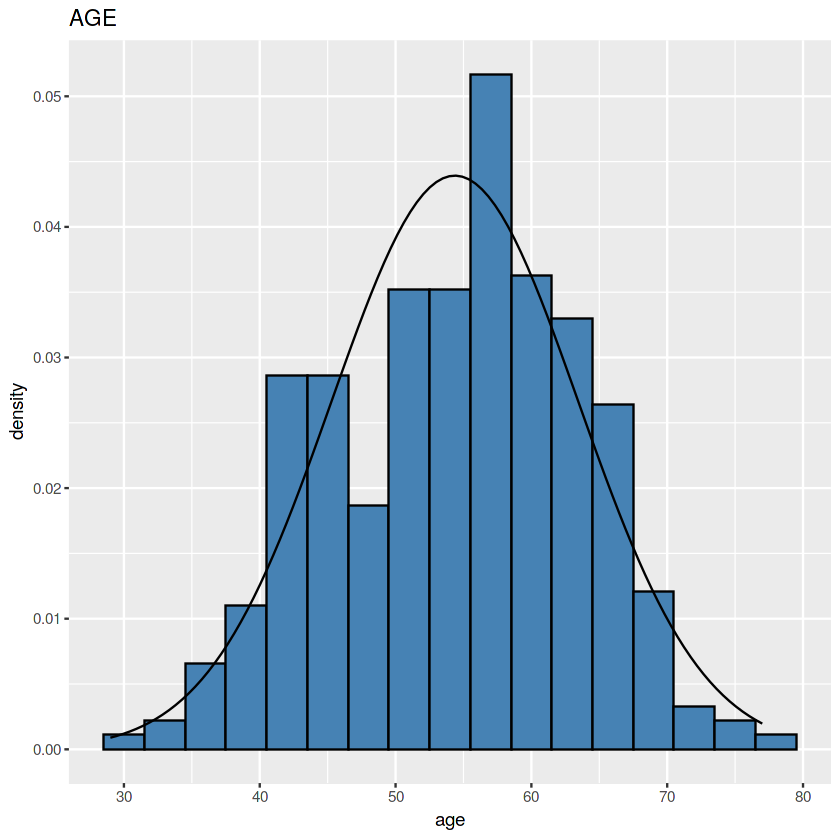
Karena ada kolom umur, sekalian saja kita uji apakah umur pada data UCI memiliki pola lonceng juga.
datum <- uci[c('age')]
ggplot(datum, aes(x=age)) +
geom_histogram(mapping=aes(y=..density..), fill="steelblue", colour="black", binwidth=3) +
ggtitle("AGE") +
stat_function(fun=dnorm, args=list(mean=mean(datum$age), sd=sd(datum$age)))
Ya lumayanlah.
Tekanan Darah
datum <- uci[c('trestbps')]
ggplot(datum, aes(x=trestbps)) +
geom_histogram(mapping=aes(y=..density..), fill="steelblue", colour="black", binwidth=3) +
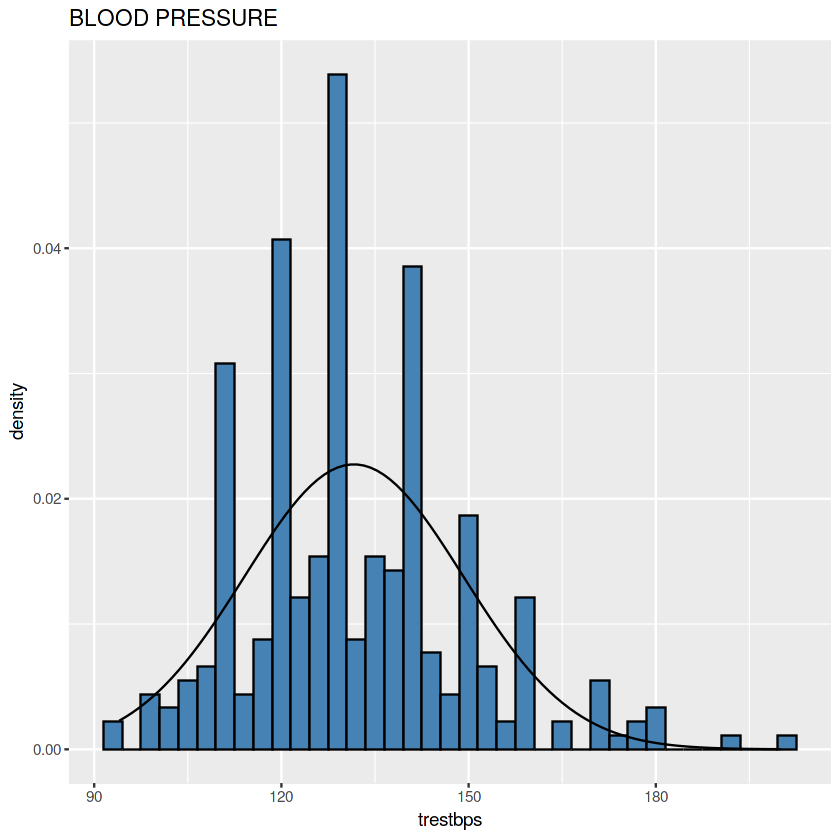
ggtitle("BLOOD PRESSURE") +
stat_function(fun=dnorm, args=list(mean=mean(datum$trestbps), sd=sd(datum$trestbps)))
Bolehlah. Agak ekstrem tapi pola loncengnya memang ada.
Open University Learning Analytics dataset
Data ini berasal dari kampus di Inggris, Open University, berisi antara lain daftar beberapa mata kuliah, rentang umur mahasiswa, aktivitas di Virtual Learning Environment, nilai mata kuliah dan beberapa kolom lainnya.
assessment <- read.csv("../input/open-university-analytics-datasets-unzipped/studentAssessment.csv")
Score
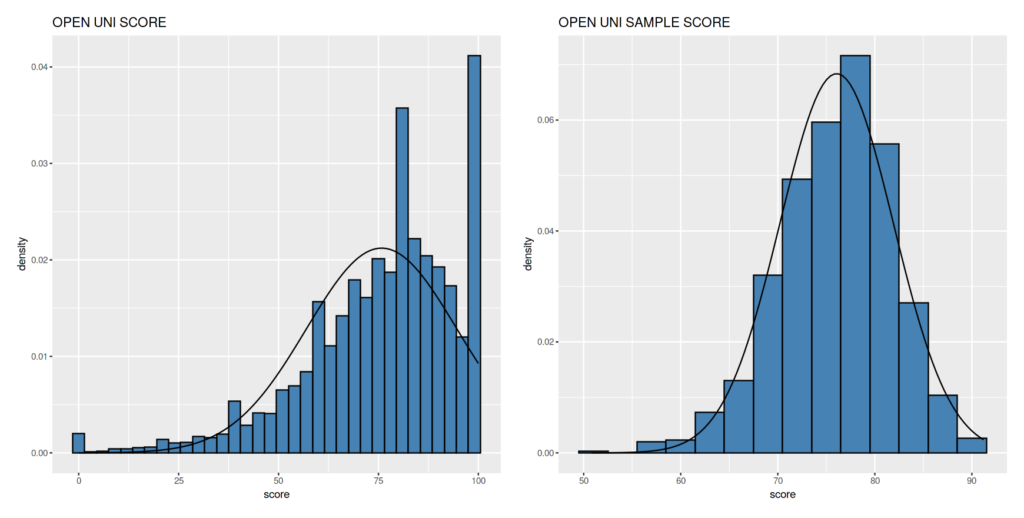
Dataset ini digunakan untuk menguji apakah nilai ujian mengikuti pola Normal Distribution, karena itu hanya kolom score yang akan digunakan.
datum <- assessment %>% filter(!is.na(score)) %>% select(score)
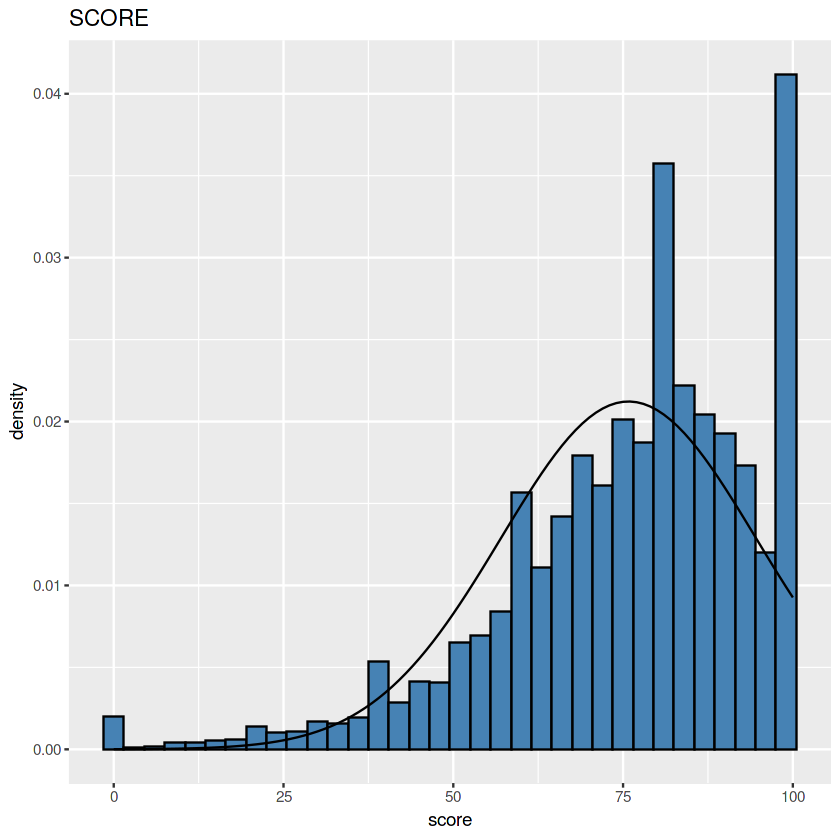
ggplot(datum, aes(x=score)) +
geom_histogram(mapping=aes(y=..density..), fill="steelblue", colour="black", binwidth=3) +
ggtitle("SCORE") +
stat_function(fun=dnorm, args=list(mean=mean(datum$score), sd=sd(datum$score)))
Cukup mirip lonceng meski nilai 100 jumlahnya banyak sekali.
Sebagian data memang mengikuti pola lonceng, meski tidak patuh-patuh amat. Tapi data umur dari Cardiovascular Disease dataset derajat ketidakpatuhannya sepertinya lebih besar ketimbang data lainnya.
Oke, untuk sementara kita “akui” pelbagai data memang terindikasi mengikuti Normal Distribution. Mengenai “derajat kepatuhannya” kita akan cari tau nanti, pasti di luar sana sudah ada orang yang membuat rumus untuk mengukur itu.
Central Limit Theorem (CLT)
Adalah salah satu terminologi yang sering muncul di dalam artikel mengenai Normal Distribution.
CLT bilang jika kita mengambil beberapa sampel (dengan pengembalian) dari populasi maka distribusi mean (rata-rata) dari sampel yang diambil tersebut akan mendekati (pola) Normal Distribution.
Contohnya dari data Umur dataset Cardiovascular Disease di atas, kita akan mengambil sampel sebanyak 10 data, menghitung nilai mean darinya lalu kita catat. Kegiatan tersebut kita ulang sampai sebanyak 1.000 kali.
get_sample <- bind_rows(replicate(1000, cardio %>% sample_n(10, replace=T) %>% summarise_all(list(mean)), simplify=F), .id="Obs")
datum = get_sample[c('age_y')]
ggplot(datum, aes(x=age_y)) +
geom_histogram(mapping=aes(y=..density..), fill="steelblue", colour="black", binwidth=1) +
ggtitle("AGE") +
stat_function(fun=dnorm, args=list(mean=mean(datum$age_y), sd=sd(datum$age_y)))
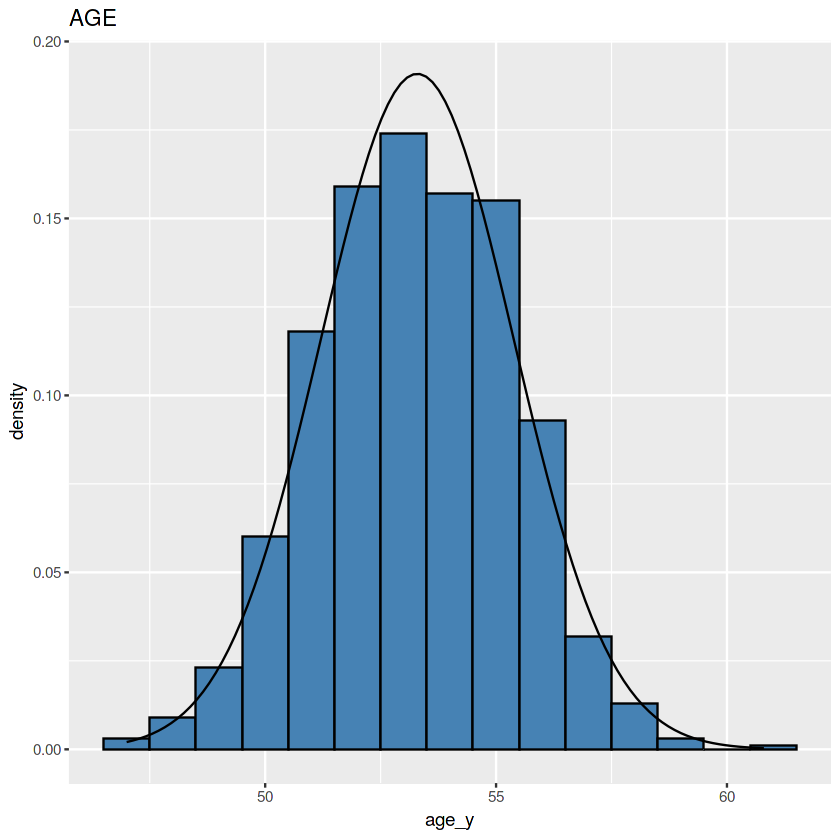
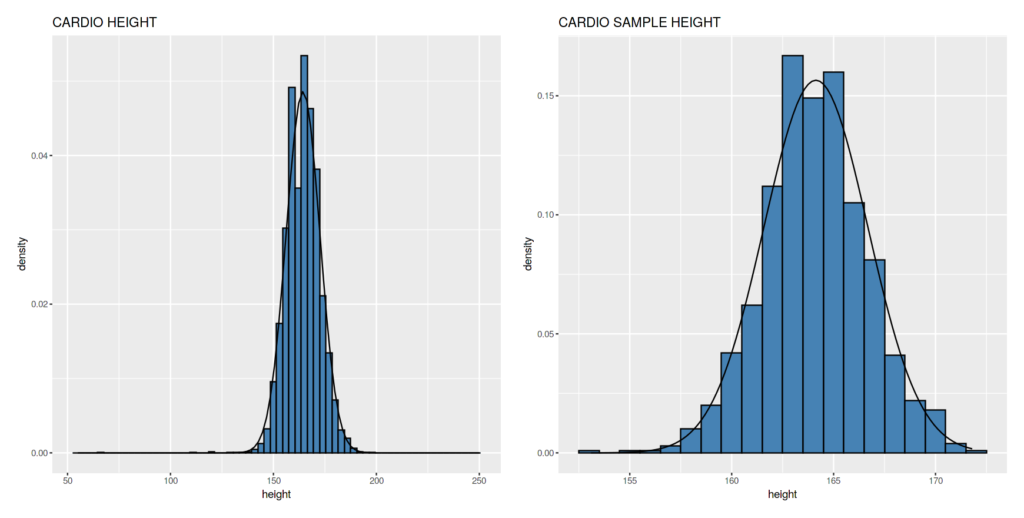
Agar lebih jelas membandingkan, begini gambar before after-nya.
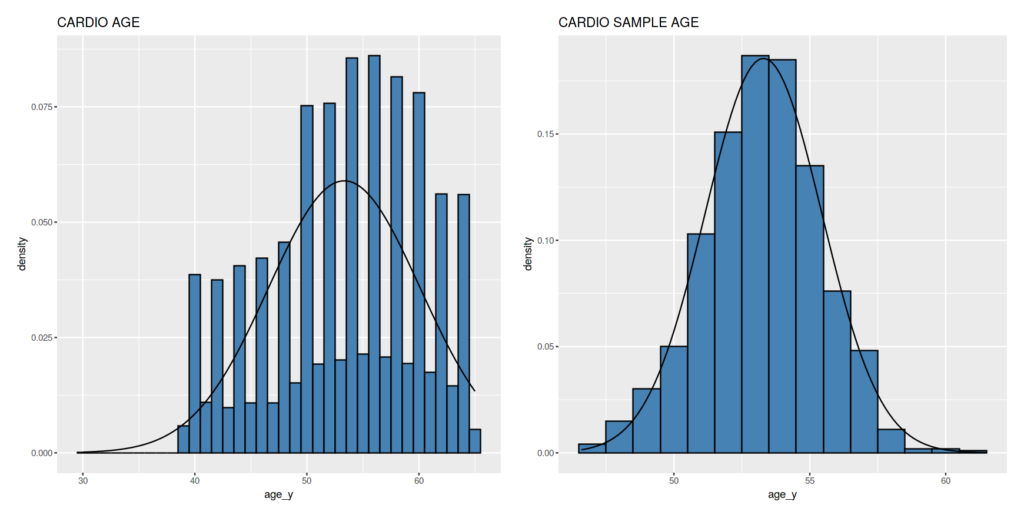
Tampak menjanjikan.
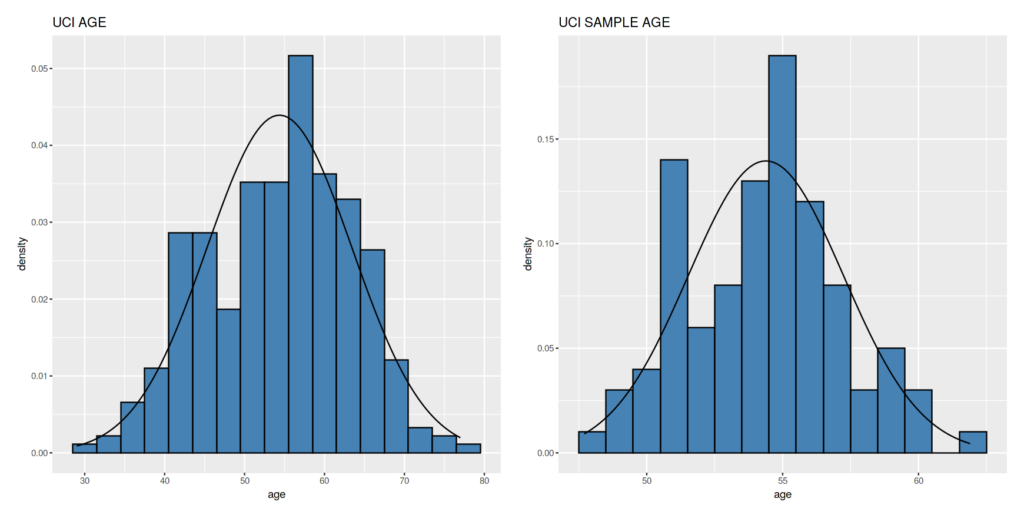
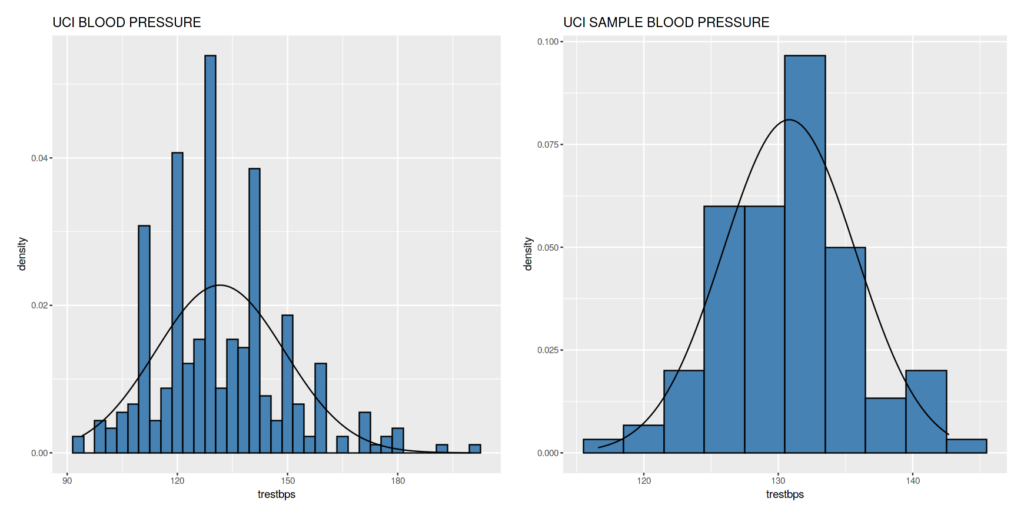
Berikut grafik untuk data lain yang diuji sebelumnya.
Distribusi nilai mean dari sampel tiap-tiap dataset memang makin mirip dengan Normal Distribution. Umumnya dikatakan bahwa makin banyak sampel yang diambil, maka distribusi mean-nya akan makin mirip Normal Distribution.
Ukuran banyak adalah jika banyak sampel alias
. Jika populasi berdistribusi normal maka
tetap menghasilkan distribusi mean yang mirip Normal Distribution.
Mean
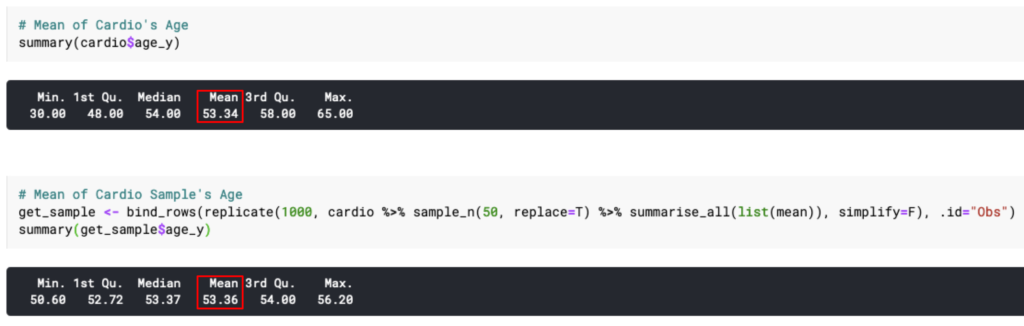
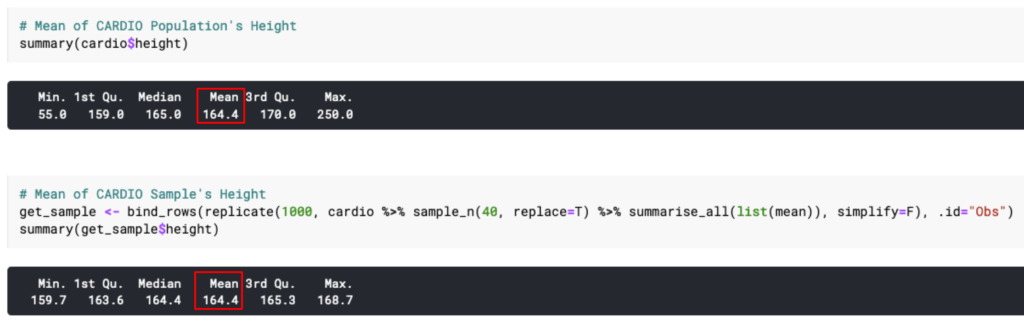
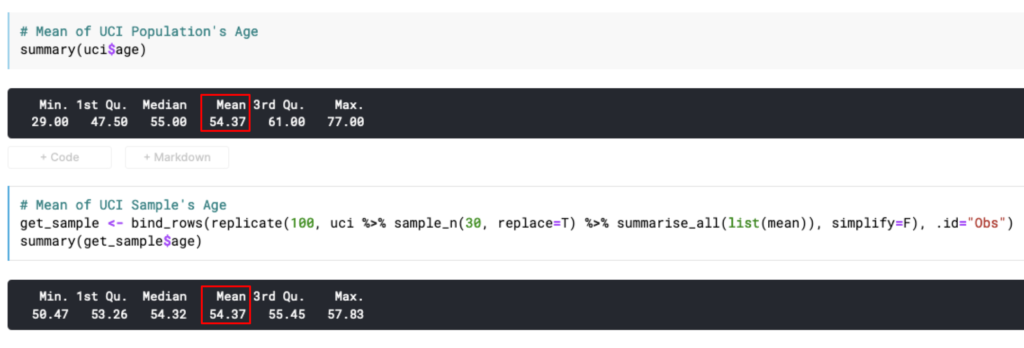
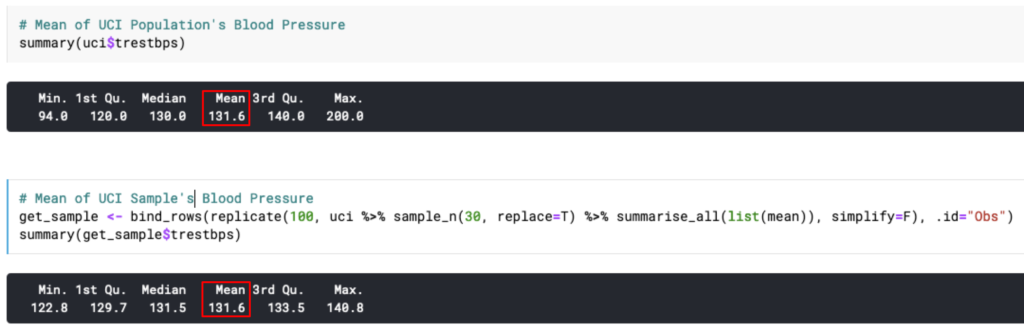
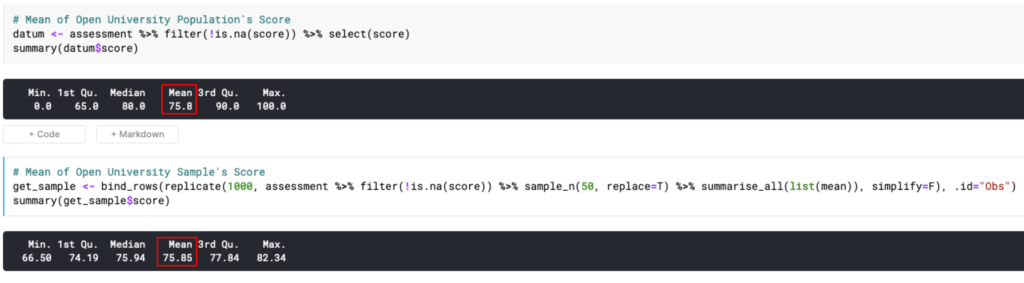
Fenomena menarik lain yang dapat ditemukan adalah nilai mean sampel akan menjadi (setidaknya mendekati) nilai mean populasi.
Tentu saja kita akan menguji klaim tersebut.
Oke, emang nilai mean sampel mendekati nilai mean populasi.
Standard Deviation
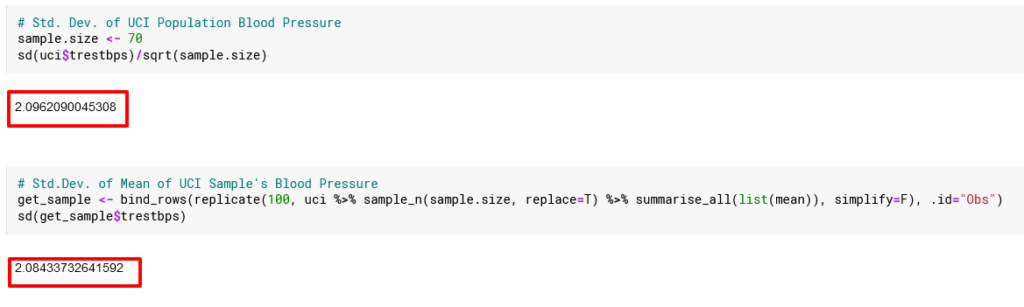
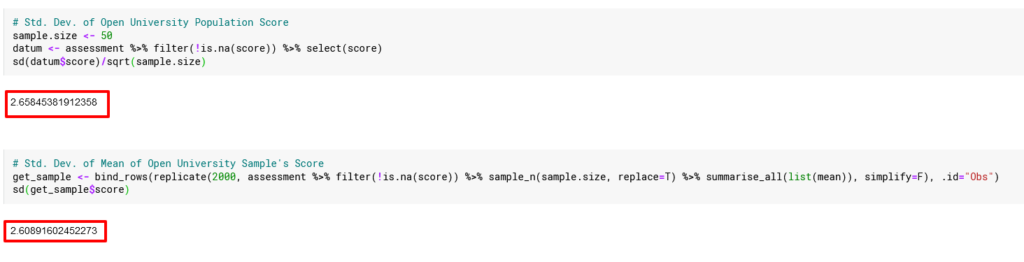
Kejutan belum usai. Nilai standard deviation rata-rata sampel (sample mean) adalah nilai standard deviation populasi dibagi dengan akar dari jumlah sampel.
Seperti biasa, kita uji.
Ada kemiripan nilai antara standar deviasi populasi dan standar deviasi nilai mean dari sampel, tidak akurat betul namun dapat diterima. Sebagai catatan, jumlah sampel akan mempengaruhi “kemiripan nilai” tersebut, karena itu mohon pembaca dapat take with a grain of salt mengenai standar deviasi ini.
Tulisan mengenai Normal Distribution masih akan berlanjut, kita tunggu apa yang menarik lainnya dari fenomena ini.
Simpulan
Normal Distribution adalah fenomena yang mudah ditemui, setidaknya Central Limit Theorem (CLT) memperjelas hal tersebut.
Langganan dan Saran
Suka tulisan di sini? Berlangganan agar kami dapat mengirimkan pemberitahuan tulisan baru. Jika punya saran, keluhan terhadap blog ini, sila ajukan melalui halaman ini.
Cover Photo by Matt Briney on Unsplash
Referensi
- https://www.researchgate.net/post/What_could_be_good_examples_of_normally_distributed_variables_that_I_can_use_to_illustrate_Normal_Distribution
- https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_probability/BS704_Probability12.html
- https://www.statisticshowto.com/probability-and-statistics/normal-distributions/central-limit-theorem-definition-examples/
- https://www.kaggle.com/sulianova/cardiovascular-disease-dataset
- https://www.kaggle.com/ronitf/heart-disease-uci
- https://www.kaggle.com/tedogogoladze/open-university-analytics-datasets-unzipped
- https://stackoverflow.com/questions/33501421/how-to-draw-normal-distribution-graph-with-two-standard-deviation-in-r
- https://stackoverflow.com/questions/60546225/plotting-the-normal-and-binomial-distribution-in-same-plot