Central Tendency

Pada tulisan sebelumnya kita telah melakukan instalasi R dan sedikit (sekali) membahas mengenai statistika deskriptif. Telah pula disebutkan bahwa kata statistika dalam obrolan sehari-hari digunakan untuk menyatakan paling banyak, atau ter ter-(besar, kecil, banyak, sedikit) lainnya. Penggunaan istilah statistika tersebut mengacu pada statistika deskriptif. Kenapa? Akan kita bahas beberapa topik dalam statistika deskriptif yang ~~sepertinya~~ membuat orang mengasosiasikan ter-ter dengan kata statistik.

Central Tendency, sesuatu tentang tengah data, metode apa yang bisa membantu kita mendeskripsikan tengah data yang kita punya. Beberapa pendekatan yang bisa dilakukan untuk mendeskripsikan tengah data kita adalah Mean, Median, Mode (modus).

Mean

Dalam istilah sehari-hari, rata-rata. Tambahkan seluruh nilai, bagi dengan banyaknya nilai.

Sebagai contoh, kita akan menggunakan data proporsi penduduk yang memiliki ponsel di daerah perdesaan yang dapat diunduh di sini. Data yang menarik dari data.go.id (ada banyak yang menarik lainnya di sana).

8.19, 12.3, 24.3, 38.2, 49.2, 61, 69.5, 75.9, 79.4, 81.3, 82.9

Data di atas adalah proporsi penduduk yang memiliki ponsel di daerah perdesaan di Indonesia pada tahun 2005 sampai 2015.

$Mean = \frac{8.19 + 12.3 + 24.3 + 38.2 + 49.2 + 61 + 69.5 + 75.9 + 79.4 + 81.3 + 82.9}{11}$

$Mean = \frac{583.18}{11}$

$Mean = 52.93$

Sesederhana itu. Namun karena penulis sedang nganggur dan ingin terlihat pintar maka kita akan membahas mengenai rumus mean.

Observasi (pengamatan) menghasilkan data, atau jika konstruksi kalimatnya diubah, data dihasilkan dari observasi. Data di atas didapatkan dari 11 observasi, dapat dinotasikan $N = 11$ .

Masing-masing pengamatan dapat diberi simbol X sehingga jika dirangkum kurang lebih seperti ini.

Observasi	Simbol	Hasil Observasi
Pengamatan pertama (2005)	X₁	8.19
Pengamatan kedua (2006)	X₂	12.3
Pengamatan ketiga (2007)	X₃	24.3

Mean sendiri dapat dinotasikan dengan $\overline{X}$ . Sehingga rumus untuk mean adalah.

$\bar{X} = \frac{X_1 + X_2 + X_3 + ... + X_{N-1} + X_N}{N}$

Jika dirasa terlalu panjang, kita dapat menggunakan simbol penjumlahan $\sum$ (sigma kapital).

Untuk menambahkan sejumlah N observasi ( $X_1 + X_2 + ... + X_N$ ) kita dapat menuliskan sebagai.

$\sum_{i=1}^N X_i$

Rumus mean yang disingkat adalah.

$\bar{X} = \frac{1}{N}\sum_{i=1}^N X_i$

Sekarang bagaimana jika ingin melakukan perhitungan di R?

Seperti pada tulisan sebelumnya saat mencoba pertama kali R, kita akan langsung menuliskan kode di R Console.

> cellular <- c(8.19, 12.3, 24.3, 38.2, 49.2, 61, 69.5, 75.9, 79.4, 81.3, 82.9)

Menginisiasi variabel cellular yang diisi dengan vektor (kumpulan angka) dari data proporsi penduduk perdesaan pemilik ponsel.

Untuk mengisi variabel (variable assignment) kita dapat menggunakan operator <- dan = namun disarankan untuk menggunakan <-. Sedangkan c() adalah fungsi untuk mengkombinasikan nilai(-nilai) menjadi vektor.

Untuk mendapatkan mean kita dapat menggunakan 2 pendekatan, hitung sendiri dan pakai fungsi. Untuk hitung sendiri.

> sum(cellular)/length(cellular)

Kode di atas membagi jumlah vektor cellular dengan banyaknya data. Lupakan perulangan (looping) seperti yang dilakukan di bahasa pemrograman lain, karena R dikhususkan untuk statistik maka cukup satu kata untuk mendapatkan hasil penjumlahan semua data. Hasil kode di atas.

[1] 52.92636

Dan lebih baik lagi, R telah menyediakan fungsi untuk mendapatkan mean, itulah pendekatan kedua kita.

> mean(cellular)
[1] 52.92636

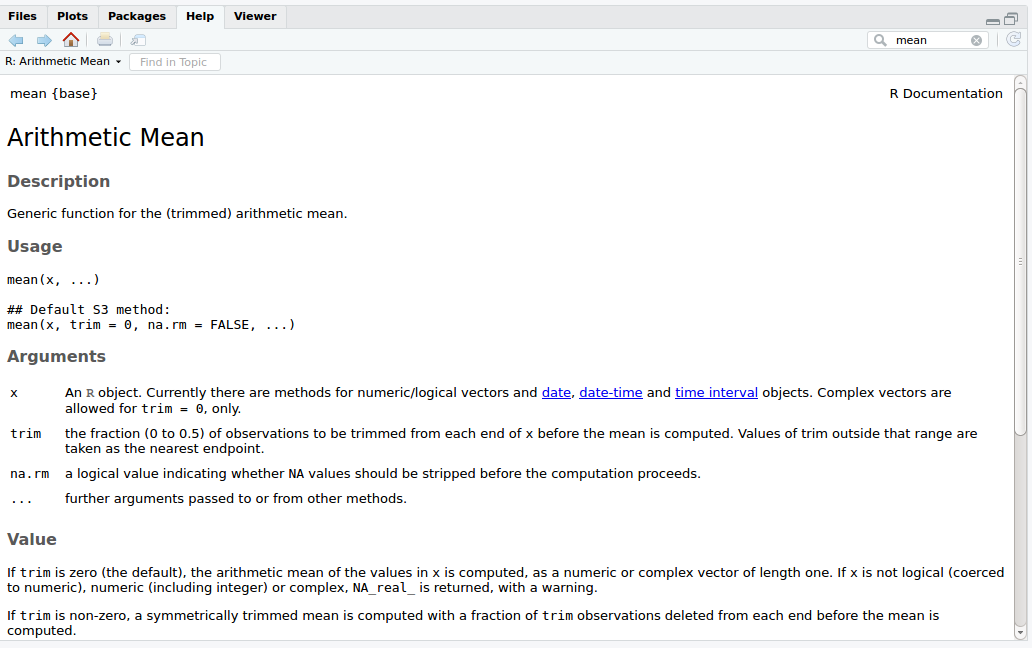
Hasil kode di atas sama persis dengan kode sebelumnya. Silahkan merujuk pada dokumentasi R untuk mengetahui fungsi-fungsi di atas, misal untuk fungsi mean ada di sini. Jika koneksi internet sedang terkendala dapat pula menggunakan menu help yang ada di panel no 4 RStudio.

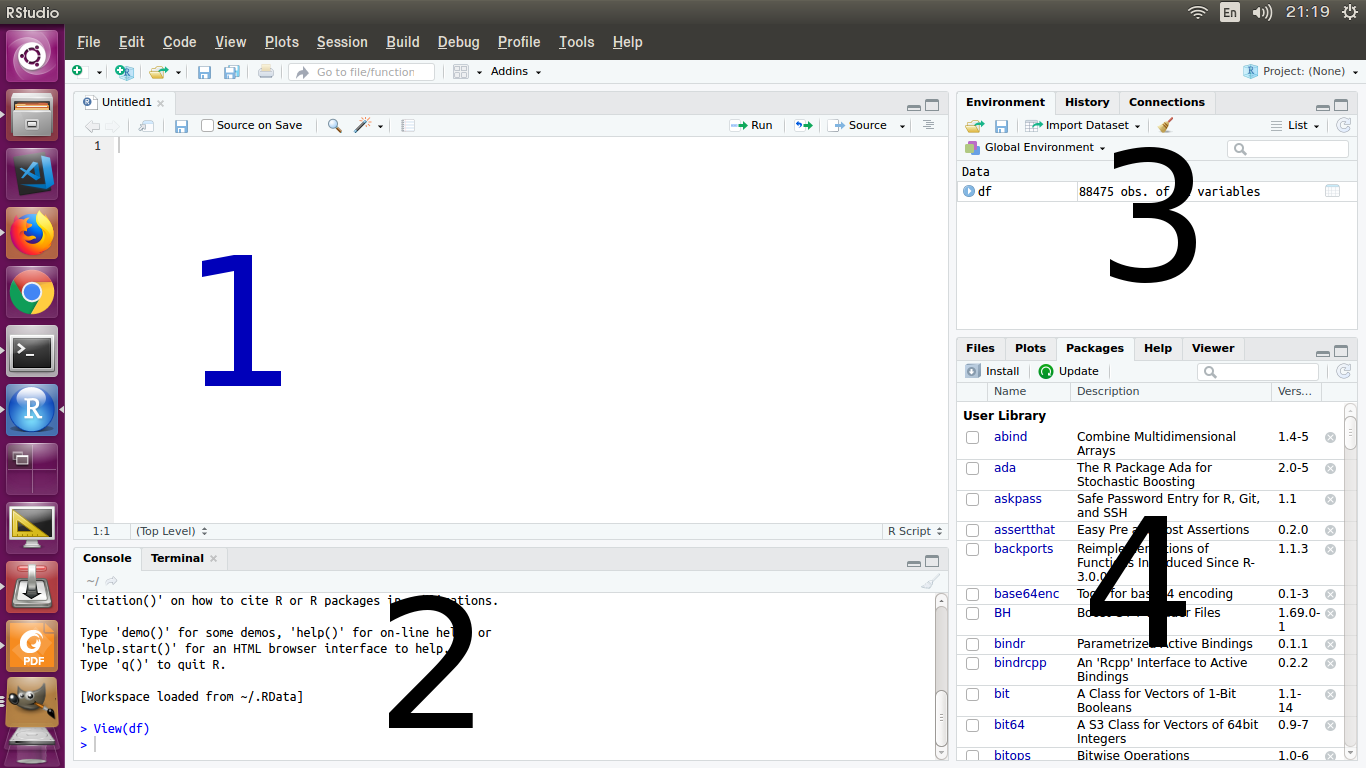
Cukup mengetik kata yang dicari, mean pada kotak pencarian di kanan atas panel.

Median

Alias nilai tengah. Urutkan dulu data dari nilai terkecil, lalu ambil nilai di tengah-tengah.

Misal kita punya data, setelah diurutkan.

8, 12, 13, 15, 17

Maka 13 adalah median. Jika jumlah data adalah genap seperti ini.

8, 12, 13, 15, 17, 18

Median adalah 13 dan 15 dibagi 2, yaitu 14. Kita uji dengan R.

> data1 <- c(8, 12, 13, 15, 17)
> median(data1)
[1] 13
> data2 <- c(8, 12, 13, 15, 17, 18)
> median(data2)
[1] 14

Sedang median untuk data ponsel perdesaan di atas adalah …

> cellular <- c(8.19, 12.3, 24.3, 38.2, 49.2, 61, 69.5, 75.9, 79.4, 81.3, 82.9)
> median(cellular)

Mode

Dalam bahasa Indonesia, modus, adalah nilai yang paling banyak muncul, ato statistik dalam konteks bahasa sehari-hari.

Misal kita mengikuti reuni sekolah, dari 10 teman yang kita temui, berikut minuman yang mereka pilih.

> drinks <- c("putih", "putih", "teh", "orson", "teh", "orson", "orson", "soda", "orson", "orson")

Untuk mengetahui nilai terbanyak kita dapat menggunakan fungsi table (kegunaan utamanya bukan itu, tapi kita pragmatis saja).

> table(drinks)
drinks
orson putih soda teh
    5     2    1   2

Seperti terlihat, ternyata sirup orson masih populer di kalangan tertentu. Hihihi.

Selingan

Kita perlu waspada dengan mean/rata-rata karena metode ini sensitif terhadap nilai ekstrim (outlier). Contohnya dari 10 teman yang kita temui penghasilan per bulan mereka dan rata-ratanya adalah seperti berikut.

> salaries <- c(7, 8, 9, 10, 8, 6, 5, 15, 9, 10)
> mean(salaries)
[1] 8.7

Ternyata ~~rerata~~ teman kita berpenghasilan 8.7 per bulan. Jika kemudian datang teman lama yang berpenghasilan 100 per bulan maka nilai rata-rata berubah.

> salaries_2 <- c(7, 8, 9, 10, 8, 6, 5, 15, 9, 10, 100)
> mean(salaries_2)
[1] 17

Nilai rata-rata 11 teman kita menjadi 17, padahal hanya 1 orang saja yang memiliki penghasilan lebih besar atau sama dengan 17, kesepuluh sisanya (mayoritas) berpenghasilan kurang dari itu.

Karena itu kita perlu hati-hati jika ada klaim yang mengatakan, “rata-rata penghasilan alumni sekolah XYZ sebesar 17 per bulan, yang mana lebih besar dari pendapatan per kapita Indonesia“. Bisa jadi nilai tersebut didapatkan dari nilai ekstrim yang sebenarnya hanya terjadi pada bagian kecil dari observasi data.

Salam.

Photo by Pixabay from Pexels

Lebih lanjut:

Published by Aan Subarkah

One Reply to “Central Tendency”

Leave a Reply Cancel reply